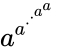A Valentine's Day Card

Giving something meaningful each Valentine's Day has become a sort of tradition between Katherine and myself.

This year, Katherine has truly outdone herself. Her handmade card quotes Carl Sagan's Demon-Haunted World, showcasing a principle that has guided my life ever since I first became a skeptic some twenty odd years ago. It's a principle that I've held close to my being and that has been at the heart of many conversations Katherine and I have about so many different things. She writes that the balance between openness to new ideas and ruthless skepticism is a dance where each of us often switch sides in our cooperative search for truth. Alongside the quote, she has made literal pinpricks of light, referencing the lone lights in the darkness that rational thinking helps us to uncover. These represent the deep truths that lie within the deep nonsense — the very same deep truths that we slowly aim to uncover as we dig through the arguments about the problems of our time.

Upon opening the card, we see that there is yet another layer to the quote on the cover. She says that I brighten her life, implying that, at a different level, the darkness of the card itself also represents our lives, separated, and the lights we have managed to uncover are the shining moments we have made in the course of our relationship. All of this is said within the confines of a Sierpinski triangle, a fractal shape of crystalline regularity that reveals yet another layer of meaning: here, the balance is in the construction of the shape, with its open spaces throughout (literally it has an area of 0) and the numerous lights that we nevertheless uncover via the application of strict logical rules within the triangle itself. It is a saga that shows us the things we can count on even within a field where nothing can be counted on. Here, she implies, is where our love resides.

On yet another layer of interpretation, we see that the lights themselves overwhelm the structure of the sierpinski triangle. The triangle itself is drawn in a dark color that is difficult to see on the black background even with the lights turned off — once they are turned on, it becomes impossible to see the logical order belying them. Only the front of the card, written in reflective ink, remains visible to the human eye when the lights wash out the scene on the dark void itself. Yet even then it is a difficult thing to make out: you must struggle to see the path before you. Ironically, it is the brightness of the lights, not the darkness of the background, that makes this so difficult. This, again, is in reference to our relationship: so many of our brightest moments sometimes overshadow our typical moments in life, and make it that much more difficult to see the structure beneath it all when we reside day by day.

I am completely taken aback at the various layers of meaning weaved into a single card. So many of our conversations over the past years point back to many of the points made on the card itself. I am sure that, to any other person, this must look just like a black card with lights embedded within. But, to me, I see the threads of our relationship here: the discussions and presented arguments, the successes within a background of seeming impossibility, and the simple joys that overwhelm even the lowest of lows in a relationship of this magnitude.

I don't know how I can top this, but I will have to up my game next year.

See also the Puzzle Portraiture she made for me, the screen print of The Tuft of Flowers, & her drawing of Jasper and the Amiibo. You can see more of her work at KatherineHess.com.

The Reality of My Dreamscape

We should not fall prey to the typical mind fallacy. Our minds are not so similar as we at first think.

Robin Raven trying to protect the innocent.

My friend Robin became vegan very early on because she saw fellow consciousness everywhere. As a young child, she cried when a Halloween-carved pumpkin would be thrown away because she deeply felt that having a face was sufficient for a being to have feelings. This experience was not typical, and it took her until high school before she internally understood that other people didn't feel the same way.

Katherine is a supertaster. She didn't understand that this was a different way to be when she was younger. She was called a picky eater because she'd turn down certain foods that she didn't like the taste of. Those foods, if tasted, would linger for days, tainting all other meals. I've gone with her to fast food places and watched mesmerized as she could identify all the foods made previously on the same grill as the item she was eating. As a child, she wanted most of all to make others feel okay, so she would often sacrifice her own desires when others were arguing -- whether this was choosing who got to sit in the front seat, deciding who had to take "the high road" when friends or family got nasty, or even just "sucking it up" and eating what was given to her even though it tasted vile. Adults around her would say: "We all have to sometimes eat stuff we don't like", but they did not understand. For her, the taste lingered. It was significant and primary. Katherine was a supertaster, and this was a big deal. She describes with relish the day she first found out:

You can test if you're also a supertaster.

I was in Europe on vacation and every meal had fish. I abhor fish. I ate it anyway, because I didn't want to rock the boat. Days later, over a breakfast that I ordinarily would have loved, I mentioned to others how the fish was still so pungent to me that it was ruining what would have been an excellent breakfast. To me, this was commonplace; it happened all the time in my life whenever I'd give in and eat something disgusting. But the surprise on others faces clued me in on the reality: other people do not have this same internal experience of taste.

 

Bebeflapula explains different levels of phantasia.

For me, it is my dream world which differs from so many others. I have aphantasia, and so cannot visually imagine anything at all in my waking life. But when I dream, I have full access to visual imagination. I'm also a lucid dreamer: unlike most people I get to choose what happens in my dreams. Unexpected things do happen there, but I have at least the illusion that I get to choose how I react to things that happen in my dreams. The combination of aphantasta with vivid lucid dreams is that I grew up valuing my dream worlds much more than other people do.

To me, the worlds that I visit when I sleep are alive. They feel like real spaces that truly matter. They aren't fuzzy or indistinct, like I see them portrayed so often in movies or when others describe their dreams. Rather, they are much more solid and distinct than anything at all that I can imagine in my waking life, and since I wear glasses they also appear much less fuzzily and as though they have a strength of reality to them that the actual real world lacks. Combine this with the fact that I get to explore that world just as lucidly as I get to explore the waking world, and you get a hyperrealistic upside-down conception of existence where the waking world just feels inferior to the dreaming world. At a gut basis, naively, I just feel as though the two worlds are equally valid and valued. The waking world is more fuzzy and less distinct, but it has continuity between every day, which I value. And the dreaming world is more solid and feels more real, even though I only get to revisit places intermittently as I return to well-known old dreamscapes.

From the now defunct study-hack site.

Of course, I understand that that the dream world is not real. But it took many years for me to get to a point where I was actually acting that way. Getting glasses for the first time as a child was a surreal event: all of a sudden the waking world started looking like the dream world did when at a distance. Glasses made me start to value the waking world much more in a way that I don't think happens with many other people. Later in life, I would tolerate living situations that many people would not be able to stand, because in dream life things could be fixed so much more easily than in waking life. Yes, I'd have to tidy up in both worlds, but, in one, I could but make the intention to do so, and it would happen, just as a nose-twitching witch might; but, in the other, tidying up meant actually taking the time to do so. When both worlds felt (naively) equally valuable to me, you can imagine that this resulted in me prioritizing the effects that occurred in my dream life over those that I built in my waking life. Many times in my life I would accept squalid conditions in one if I had good conditions in the other, merely because, to me, both were real.

It wasn't until I understood that aphantasia was a thing in mid-2020 that I finally realized what was going on here, I had had the typical mind fallacy for so long that it just hadn't occurred to me that the reason I valued dream life so strongly was because there I could visualize, even though I couldn't anywhere else.

Today, I finally value the waking world more. But it is a thoughtful decision that I do so; it still feels naively as though they should be equally valid. I just realize that this is a wrong thing to think now.

Yesterday, I had a nightmare, Jasper's dead body had come home. We were mourning when suddenly his body moved, and I heard the smallest of sneezes. I rushed to him, horrified to realize that maybe the euthanasia had not worked, and when I got next to him, his head raised, looking at me with the most expressive face. It was a face of unbridled pain. He was suffering physically, but more than that, it was a look that showed he felt betrayed. Why had I not fought harder to help him to live? Didn't I love him? Why had I caused him to die, and to suffer these many days in pain away from his family?

I screamed, waking up both myself and my partner. I was sweating. I looked over to the box where Jasper's remains actually lay in the waking world. I cried. Katherine reminded me that Jasper lived a happy life, right up until the end. I had not betrayed him. Jasper loved me. Slowly, I calmed down.

Nightmares for me are thankfully rare. But when they happen, they are horrendous. I don't think I can successfully explain just how real they are to me other than to point out that my dream world naively feels more real than my waking world. It is only with intellect that I understand the waking world to be more real than my dream world. Nightmares, to me, are true horrors second only to the waking world horrors one learns of in rationality or effective altruism circles.

From Corey Mohler's Existential Comics.

When I speak to people in my life, I'm not likely to mention any nightmares I have. It doesn't come across well. Others have nightmares, too, but their nightmares don't seem to have that same feeling of reality that mine have. My nightmares linger. For others, a dream passes quickly from the mind. Mine do, too, in the specifics. But, unlike others, when I sleep again I go back to the same place, and the specifics come back to me. An area previously explored has some changes, but the layout is the same. The rules are the same. I get to talk to the different people that are there, and visit the areas I care about most as often as I want, even years later when I return to that same dreamscape. Over time, the memories of these repeated dreams linger in my waking world memories. Even now, I can tell you about a certain dream place that I have gone to dozens of times, even though I haven't visited in the past year or so, where certain people live, where the decor is a certain way, where a path leads from the back door through the woods, where the path diverges to different locales depending on where I want to visit.... I know this dream place well because I've gone there so often. It's real to me. And so even though I have only had this Jasper dream once, I feel fear. Because it has been 24 hours now and I still remember every detail. I remember Jasper's tortured face. I remember feeling that it was my fault. I remember not fighting for his life.

There are even more reasons to stay up for me now. I don't want to go to sleep.

Remembering Shawn Allin

Shawn at the Tikal Mayan ruins in Guatemala.

This will be the fourth blog post in a row that I've written about death, euthanasia, and/or suicide. Maybe you, the reader, will think this is a sign that I am focusing in an unhealthy way on these issues ever since Jasper's death last week. Well, maybe I am. It's been a difficult time for both Katherine and myself. Every time we reach over to pet Jasper only to find an empty armrest, it is a newly punched hole in our collective ability to be okay with how life is now.

However, this time I have an excuse. A few days ago, I received an email from someone asking me about my memories of Shawn Allin. Shawn was my friend, teacher, and mentor. His first day of teaching classes at Spring Hill College was also my first day of taking classes there. We hit it off immediately. Four years later, my final days at Spring Hill College were also his final days. Except instead of moving on, as I did, to places beyond the university, he died suddenly in his office, possibly of suicide.

Carpe Diem is near Spring Hill College.

I'm calling him Shawn now. It's weird because of course I'd call him Shawn now. We were friends. But when I met him, he was Dr. Allin to me, and when I think of him today, that's the name that pops up in my head. Still, I'll try to address him as Shawn here, as he undoubtedly would be addressed by me today, had he ended up living.

I knew only a small part of Shawn. I never visited his home. He never talked with me about his passion for motorcycles (nor of his apparently quite rad motorcycle helmet with satanic goat images airbrushed on it!). I never asked him about the rollerblades he used to travel on campus. We never discussed the obscure punk musical albums displayed in his office. The only times we had dinner together was when we both stayed late in the Chemistry building doing work of some kind. (I would help to analyze and graph data from his and his upper-level students' experiments.) But we did have lunch occasionally, and we would meet for afternoon tea at Carpe Diem. He would loan me countless books, which we'd then discuss later that week. We were close enough that when summer break came, he invited me to come with him to the badlands of South Dakota to dig for dinosaur bones. 

Shawn w/ Fr. Michael Williams
blessing Quinlan Hall in 2003.

But we never really talked about his personal hopes and dreams, nor the problems he was having after his divorce with his depression. I didn't learn about these things until after he died. Throughout the time I knew him, he kept his personal problems separate from his interactions with me.

Does this make me less of a friend? Or perhaps he had a personal rule not to fraternize too closely with students at the institution at which he worked? I don't know. I can't know. But he was certainly a friend to me, and I very much enjoyed his company.

The person who emailed me a few days ago asked me to tell a few stories about Shawn. I was given permission to also share those stories here, on my blog. These small stories come partly from the small sliver of his life that he chose to share with me, but also from the long discussions I had with others after his death.

Shawn's first class at Spring Hill was also my first class. This coincidence, alongside the fact that I was more of an adult than his other students (I was 21), meant that he ended up singling me out as an initial friend at the school. I remember going to his office after that first class and being amazed at all the cool knickknacks on his desk. There were mathematical structures, models of chemical bonds, simple physics machines…. But also there was a plethora of books.

Books were one of Shawn's things. He had a number of varied interests, and so obviously you might expect him to own books on several different topics. But he didn't just own the books in order to have the content at hand; he liked books for books' sake. Each book was treated extremely well. There were no marks within, no dog-eared copies. But you always could tell his books apart: he would emboss the title page of every book in his possession with his name: From the library of Shawn B. Allin. It was the only mark that you'd ever find in any of the books in his collection.

Shawn w/ Gregory Morgan at Rydex Commons

Nevertheless, within an hour of meeting him, he had already decided to loan two of his books to me. I was honored, especially as he gave a stern warning about how well to treat them. The first was The Panda's Thumb, by Stephen Jay Gould. I adored it. Gould was an excellent writer and Shawn was absolutely perfect in picking that first borrowed book to entice me to keep coming back for more. (After Shawn died, his family gave me his copy, which I treasure to this day.) The second was In Search of Schrödinger's Cat, by John Gribbin, which also enamored me. He had caught on quite quickly to my prior interests in quantum physics and skepticism, and chose perfectly to suit my interests. I stayed up half the night reading both books and returned them first thing in the morning before classes started. Upon their return, he smiled gently: "Eric," he started, in his distinct Canadian accent, "I anticipate this will be the start of a great friendship."

He continued to loan me books every week until I had exhausted the portion of his library that was suitable for me to read. (I turned down the motorcycle and punk rock books.) It was a tradition that lasted years, well after I had ceased taking any classes with him. In fact, I only took two classes of his in my freshman year. All of my interactions with him afterward were solely due to our friendship.

• We toasted to the ill-fated Superconducting Super-Collider.
• We discussed changes in our understanding of quasars, which were only just recently discovered to be different than how they were described in the books I had previously read about them.
• We talked for hours about skepticism and its role in society; about Carl Sagan's excellent The Demon-Haunted World; and after he died, I attended several skeptic conferences like The Amaz!ng Meeting, where I met several of the authors whose books he had lent me.
• In class, he would jump onto a chair to reach up high to the periodic table behind him and explain why it's grouped into four blocks, talking with a glint in his eye that showed his dedication to the topic.
• He told me privately that my being a 21 year old freshman was a good thing, because my life experience is priceless: I appreciated college whereas so many other students did not.
• Once, when we spoke of philosophical concepts that might not make sense, he argued that 'nothing' as a philosophical concept could only be the absence of properties, and could not properly be attributed properties in itself, as I was claiming at the time. (I have since come around to his point of view on this, but only much, much later, for different reasons than he was arguing.)

Gumbo Buttes of the Badlands.
I stayed w/ Shawn here to dig dino bones.

Despite being otherwise close to him, I didn't spend much time around Lynn, his wife. I'm not sure if he intended to keep these parts of his life separate, or if it was just happenstance. But every time I saw them together, he would use me to illustrate some point of his. I recall once that he had been having some friendly argument with Lynn, claiming that lots of people knew what buckyballs were. Lynn didn't believe him, so when I dropped by, he picked a buckyball model from one of his shelves and loudly asked: "Eric, tell Lynn here that you know what the name of this object is." I froze, stammering, and Lynn laughed: "See? No one knows what a buckyball is. You're just a bad judge of what is common knowledge."

1000 miles from Spring Hill College,
we traveled on this road in the Badlands.

Shawn helped to organize events that would help the students learn more about social justice. He set up a viewing of the movie Hotel Rwanda once in the main hall, and he'd often organize students around Amnesty International interventions. I can remember my fingers hurting after stuffing envelopes for hours; if I think long and hard, I may even be able to remember Condoleezza Rice's office address at the time. (My fingers hurt now just thinking about it.)

I suspect the divorce hit him hard. I can't say for sure, because he never talked about it with me. But a common friend of ours, Bill, was someone that he did confide in. I can relay a few things that I learned from Bill, though I learned these things only after Shawn died.

Covered w/ dirt for 65m years, but only
a few days in the sun bleached these bones white.
Another few weeks would ruin them.

Shawn had been dealing with bouts of depression for as long as Bill knew him. In 2001, these became more regular and more intense. He sought medical treatment for his depression, but it was sporadic at best. After the divorce (the summer before he died), Shawn spent three weeks in Marmarth, ND, with Bill. Bill has a place in Marmarth where he stays while he is doing fossil prospecting; I visited there in the summer previously with Shawn.

I wasn't there during those three weeks, but Bill says that Shawn was not only depressed, but also full of hatred. He was angry at his situation, at his marriage falling apart, and even at his fellow faculty. According to Bill, he had felt that he had found a home among like-minded faculty with a similar high level of standards, but for the previous year he had been very hard on his colleagues for not attaining the levels that he thought they should. Bill seemed to think that this feeling was borne more out of his depression than from how his fellow colleagues actually were. I can offer no opinion on this, because Shawn always hid this side of himself from me. But it was bad enough that he accepted a position at Monmouth College in Monmouth, IL, and was planning to leave Spring Hill College at the same time that I was.

He never ended up moving there, though. He died suddenly, in his office, only a month or so after accepting the position at Monmouth.

This is after digging for a bit.
Had I known he was going to die, I would have prioritized
taking photos with Shawn in them, rather than just of the bones.

I don't actually know what happened. His death could have been accidental. Certainly, it seems strange to accept a position elsewhere, earnestly go looking for a new house, and then to so quickly decide otherwise. But Bill believed his death may have been intentional. Certainly, if it was suicide, it was not due to his rational thought. Shawn most certainly had depression and had had it for a very long time. I never saw that side of him; he kept his depression hidden in all of his actions as a teacher. But his closer friends, like Bill, knew, and I wish so much that he had just figured out something that could have dealt with these extreme emotions pharmaceutically.

I should also mention that another very close friend of his does not believe it was suicide. They were high school sweethearts a long while previous, and had been talking again after Shawn's divorce. Mere hours before he died, he sent a very normal-seeming email to her. This may be taken as strong evidence that what happened was an accident, and not intentional. If there was a suicide note, it was kept private and I was never informed of it. I also know that he had just filled a new prescription the previous day for pneumonia. Maybe it was an allergic reaction? But, if so, this was never stated to be the case publicly. On balance, I believe that it was likely suicide.

Near Marmarth, ND.

In those days, I didn't have a mobile phone. As such, I don't have any personal photos of his office, nor of his person. The photos you see here are all that I have of him. All are taken by other people. It's strange, looking back on them. I have aphantasia, and so have a terrible memory for faces. Nevertheless just glancing through these photos immediately brings me back.

Shawn was my teacher. I didn't end up going into science, like he wanted, but when he learned that I'd switched to a double major in philosophy and mathematics, he would debate me endlessly on philosophy of science, Bayes' theorem, and the limits of what we can know. We were both staunch atheists, but for some reason we never talked about it. This may be because I was a student at (and he was a teacher at) a Jesuit university, and he seemed to have personal rules about what is or is not an appropriate topic of conversation with one of his students.

Shawn loved tortoises.

I don't know a whole lot about his life outside of Spring Hill College. But I did know him as a friend and mentor, and he definitely inspired me in particular to do and be a better person. I do not think that I would be as successful as I am today if it were not for some of his influences. His push for social justice in particular helped me to realize the direction of where I ended up today.

I'd also like to share a few other aspects of Shawn that the person who emailed me might not be aware of.

Shawn published 31 times in various chemistry journals. Five of those have been cited multiple times, and one, on the Solvent Effects of Molecular Hyperpolarizability Calculations, has an astonishing 47 citations today, 8 of which occurred within the last year. (For reference, a mere 10 citations already puts your work in the top 24% of the most cited work worldwide; 47 citations brings you closer to the top 3–5%.) This means that the work that Shawn provided to the scientific community lives on to this day.

But, I'm memorializing GT & Dr. Allin in my dissertation. Sending <3 to my #sprhill Fam today @sprhill @SHCALUM (2/2) pic.twitter.com/tA0ewp0kJM

— Dr. Kat Patterson (@MarineKatPat) April 18, 2015

Our department was well represented yesterday at Honors Convocation and Undergraduate Research Symposium. Dr Allyn...

Posted by Spring Hill College Department of Chemistry, Physics, Engineering on Saturday, April 21, 2018

Shawn has been memorialized in a dissertation. At Spring Hill College, exceptional chemistry students continue to earn the Shawn B. Allin Memorial Award each year. He is remembered years later as being a huge positive influence (see page 12). Alyn Gamble wrote an excellent article about him in Volume 86 Number 10 of the SpringHillian. (If you only click one link in this blogpost, click this one. Gamble is an excellent writer, and their article about Shawn in the school newspaper was very well done.)

In the years since I posted in my blog of Shawn's passing, I've received several emails. Here are a few excerpts from them:

"I grew up with Shawn in Sarnia, Ontario and from what I can gather, he was as beautiful a person 'all grown up' as he was when we were kids.  I was shocked and saddened by the news of his passing.  Always had hoped that I would have the chance to connect with him again someday.  Your website gave me a chance to do that.  I hold him in my heart.  Thank you."

 

"I know that he valued teaching and treasured those times when he knew that his efforts mattered to students. … Treasure those times when his efforts mattered."

 

"Shawn was my first love and we dated all through high school and during our 4 years at the University of Waterloo.  I also dated Shawn while be worked at EcoPlastics in Toronto but when things didn't work out, he returned to school (University of Guelph) and I moved on with my life. … I broke my leg about 3 weeks ago and had been talking with him daily due to my limited mobility.  We spent a lot of time discussing his challenges and we reviewed, in great detail, his career decisions and his acceptance of the offer in Ill. … Shawn has told me lots about you and his other friends at Spring Hill.  He mentioned that you were a superior human being and that he enjoyed all of his discussions with you over coffee at Carpe Diem.  I now wish that I had kept all of the messages that he sent me so that you could read - in Shawn's own words - how much he liked you and appreciated you as a friend."

 

"Shawn was the Allin's pride and joy - a doctor - a professor - a brilliant man with so much potential - let them know about the gifts that he gave to you and about your friendship - that will give them comfort."

 

Shawn was 41 when he died. I will turn 40 later this year. Maybe this means it is appropriate that I remember him now, as I am the age that he was when he was still loaning me books and grabbing a drink with me at Carpe Diem. I can only hope to make a difference as much as he did in his 41 years of life.

I miss you, Shawn. Thank you for being my friend.

Most Functions with Predictive Power in the Natural Sciences are Non-Differentiable

Epistemic status: highly uncertain.

Recently, Spencer Greenberg posted three useful facts about mathematics:

Here's the most useful mathematics I can fit in 3 short paragraphs (see image). pic.twitter.com/DM2ytwelYo

— Spencer Greenberg 🔍 (@SpencrGreenberg) December 5, 2020

This generated a bit of discussion on facebook:

Here's the most useful mathematics I can fit in 3 short paragraphs (see image). -- Note: each week, I send out One...

Posted by Spencer Greenberg on Friday, December 4, 2020

In one of the comment threads, I put forward what I thought to be an uncontroversial thought: that although it is true that most useful mathematics in the natural sciences are differentiable, this is not because the useful math stuff happens to also be differentiable, but instead because we can (mostly) only make sense of the differentiable stuff, so that's the stuff that we find useful. This is a weak anthropic argument that merely makes the statement partially vacuous. (It's like saying I, who reads only English, find that most useful philosophy to me is written in English. It's true, but not because there is a deep relationship between useful philosophy and it being written in English.)

It turns out that this was not considered an uncontroversial thought:

However, I also received a number of replies that indicated that I did a poor job of explaining my position in facebook comments. (And I wanted to ensure that I wasn't making some critical mistake in my thinking after hearing so many capable others dismiss the idea outright.) To fix this, I decided to organize my thoughts here. Please keep in mind that I'm not certain about the second section on math in the natural sciences at all (although I think the first section on pure math is accurate), and in fact I think that, on balance, I'm probably wrong about this essay's ultimate argument. But whereas my confidence level is maybe around 20% for this line of thinking, I'm finding that others are dismissing it completely out of hand, and so I find myself arguing for its validity, even if I personally doubt its truth. (In the face of uncertainty, we need not take a final position (unless it's moral uncertainty), but we should at least understand other positions enough to steelman them.)

Mathematics Encompasses More Than We Can Know

Before we talk about the natural sciences, let's look at something simpler: really big numbers. When it comes to counting numbers, it's relatively easy to think of big ones. But, unless you're a math person, you may not fully comprehend just how big they can get. It's easy to say that the counting numbers go on forever, and that they eventually become so large that it becomes impossible to write them down. Yet it's actually stranger than that: they eventually get to be so big that they can't be thought of (except expressed in this way). As a simple example, consider that there exists a least big whole number such that it can't, even in principle, be thought of by a human being. Graham's number, for example, is big enough that if you were somehow able to hold the base ten version of it in your brain, the sheer amount of information held would mean that your brain would quite literally implode. Yet we can still talk about it; I just did earlier, when I called it Graham's number. The thing is: the counting numbers keep going, so eventually you can reach a number so high that its informational content cannot be expressed without exceeding the maximum amount of entropy that the observable universe can hold.

Opening one's eyes to this helps with the following realization: not all numbers are nameable. Somehow, despite being an amateur interested in math for most of my life, having thought I understood Cantor's diagonal argument after reading through it several times, teaching it to others several times, and talking about it several times, I recently learned that I had skipped understanding something basic about it that wasn't made clear to me before:

Cantor's diagonal proof shows that we can't enumerate all the reals. Wrong!(?) What Cantor really shows is only that there can’t be an enumeration of all the reals of our mathematical universe. It only refers to the merely countably many nameable reals! https://t.co/LH3tN6kjiv

— Eric Herboso (@EricHerboso) November 15, 2020

Scott Aaronson's excellent explanation on this really hits home. The parts of the number line that we can name are but countable dust among the vast majority of points that we have no way of writing down in any systematic way. We can only vaguely point toward them when making mathematical arguments and can only really make basic (unappended) statements that either apply to zero, one, or an infinite amount of them at once. We can, for example, say that a random real number picked between 0 and 1 has certain properties, but if we try to say which number it is, we must use some kind of systematic method to point it out, like 1/3 = 0.3 repeating.

Something similar is true when it comes to functions. Most functions, by far, are not nameable. They are relations between sets that don't follow any pattern that makes sense to humans. For a finite example, consider the set X:{a,b,c} as a domain and Y:{d,e,f} as the range. We can construct a function f()that maps X➝Y in pretty much any way we please. Each function we create this way is nameable, but only because it is finite. Imagine instead doing this for an infinite field, with each input going to a random output. Out of all possible functions mapping ℝ to itself, almost none are continuous, and thus almost none are differentiable. Almost all of them are not even constructable in any systematic way. They are, ultimately, not really understandable by us humans right now, which is why we don't really have people doing math work on those topics at all.

Mathematics in the Natural Sciences

So far, we've established that, in pure mathematics at least, the vast majority of functions are not understandable by humans today. Thankfully, we understand a lot about differentiable functions (and some others that are easily constructable, like additions of multiple different differentiable functions separated by kinks, stepwise functions, &c.). As has been pointed out previously, the natural world uses differentiable functions all over the place. Modern physics is awash with these types of functions, and they all do an extraordinary job, giving us an amazing amount of predictive power across the spectrum from the very large to the very small. Nothing in what I'm about to say can take anything away from that in the least.

But it occurs to me that although it is uncontestedly true that almost all the useful-to-us functions governing the natural world around us are also differentiable functions, it may be that this is true for anthropic reasons, not because of some underlying feature of ultimately-useful-functions-in-the-natural-sciences themselves.

I'm not at all sure that this would actually be true, but it doesn't seem to contradict anything I know if to suppose that there may be a great many functions governing the natural world that aren't differentiable, and that the only reason we don't use them in the natural sciences is because we can't currently understand them. They are uncountable dust, opaque to us, even if, one day, our understanding of mathematics and natural science improves enough so that may eventually use these functions to make predictions in just the same way that we currently use differentiable functions. In short: the reason why almost all useful functions are differentiable is because we really only can usefully read differentiable functions. It is not (necessarily) that the useful functions in the natural world all happen to be differentiable.

Ockham's Razor

One counterargument given to me in the facebook thread involves Ockham's razor:

They are saying that while there may be no reason that this supposition might be true, we shouldn't think that it is true because, by Ockham's razor, we should prefer the hypothesis that doesn't include these extra not-yet-discovered non-differentiable functions that have predictive power over the natural world.

Before I respond to this, I feel that I have to first look more closely at what Ockham's razor actually does. I'll quote myself from Why Many Worlds is Correct:

The law of parsimony does not refer to complexity in the same way that we use the word in common usage. Most of the time, things are called "complex" if they have a bunch of stuff in them, and "simple" if they have relatively less stuff. But this cannot possibly be what Occam's razor is referring to, since we all gladly admit that Occam's Razor does not imply that the existence of multiple galaxies is less likely to be true than just the existence of the Milky Way alone.

Instead, the complexity referred to in Occam's razor has to do with the number of independent rules in the system. Once Hubble measured the distance to cepheid variables in other galaxies, physicists had to choose between a model where the laws of physics continue as before and a model where they added a new law saying Hubble's cepheid variables measurements don't apply. Obviously, the model with the fewer number of physical laws was preferable, given that both models fit the data.

Just because a theory introduces more objects says nothing about its complexity. All that matters is its ruleset. Occam's razor has two widely accepted formulations, neither of which care about how many objects a model posits.

Solomonoff inductive inference does it by defining a "possible program space" and giving preference to the shortest program that predicts observed data. Minimum message length improves the formalism by including both the data and the code in a message, and preferring the shortest message. Either way, what matters is the number of rules in the system, not the the number of objects those rules imply.

What's relevant here is that while it is true that this argument is introducing vast new entities in the form of currently ununderstandable functions that may have predictive power, it is not introducing a new rule in doing so. Those ununderstandable functions certainly do exist; they're just not studied because studying them wouldn't be useful. So the question is: does saying that they might have predictive power introduce a new hypothesis? Or does it make more sense to say that of course some of them have predictive power; we just can't use them to predict things because we don't understand those functions. If the former, then Ockham's razor would act against this supposition; if the latter, then Ockham's razor would act against those who would claim that these functions can't have predictive power.

It's unclear to me which of these is the case. I don't want to play reference class tennis about this, but the latter certainly feels true to me. The analogous Borges' Library of Babel certainly shows that an infinite number of these non-differentiable real-world functions will have predictive power (though maybe not explanatory power?), but this isn't sufficient to say that MOST functions with predictive power are non-differentiable. I think that probably most functions with predictive power are in fact differentiable -- but I'm not at all certain about this, and that's why I'm arguing for that side. I think that others are wrong to so quickly dismiss the idea that most functions with predictive power might be non-differentiable. They're probably correct in thinking that it's wrong, but the certainty with which they think it is wrong seems very off to me. Hopefully, after reading this blog post you might agree.

edit on 10 December 2020: Neural Nets

Originally I ended this blog post with the previous paragraph, but Ben West points out that neural nets have a black box that uses functions very like what I've described to make actual real-world predictions:

My confidence in this idea has increased upon realizing that there already exist at least some functions for which we do not know if they are differentiable or not that definitely have predictive power. It's important to point out that it's still possible that this thesis is wrong; it may be the the black box functions that neural nets find are all differentiable, and, in fact, that even still seems likely to me, but I definitely now give more credence to the idea that some might not be.

Fastly Fast Growing Functions

In a previous post, I discussed Really Big Numbers, moving from many children's example of a big number, a million, up past what most people I meet would think of as a huge number, a googol, and ultimately going through Graham's number, TREE(3), the busy beaver function, infinities and beyond. I wasn't aware of it at the time, but a much better version of that post already existed: Who Can Name the Bigger Number?, by Scott Aaronson.

In my original post, I made a few errors in the section about fast growing functions. Some kind commentors helped correct the most egregious errors, but the ensuing corrections littered that entire section of the post with strikethrough text that I was never really happy with. Now, six years later, I'd like to finally make up for my mistakes.

The Goal

I'd like to name some really, really big numbers. I'm not going to talk about the smaller ones, nor the ones that delve into infinities; you can read the previous post for that. Here I just want to point toward some really big finite numbers. The numbers I'm aiming for are counting numbers, like 1, 2, or a billion. They're not infinite in size. These are numbers where, if someone asked you to write a really, really big number, these would be way beyond what the questioner was thinking of, and yet still wouldn't be infinite in extent.

Why Functions?

We always use functions when writing numbers. It's just that most of the time, it's invisible to us. If we're counting apples, we might make a hatch mark (or tally mark) for the first apple, another hatch for the second ("‖"), and so on. This works fine for up to a dozen apples or so, but it starts to get pretty difficult to understand at a glance. You might fix this by making every fifth hatch cross over the previous four ("卌"), but you quickly run into a problem again if you get too many sets of five hatch marks.

It's easier to come up with a better notation, like using numerals. Now we can use "1" or "5", rather than actually write out all those hatch marks. Then we can use a simple function to make our notation easier to follow. The rightmost numeral is the ones place, then next to the left is the tens place, and the next to the left is the hundreds place, and so on. So "123" means (1*100)+(2*10)+(3*1). Of course, I'm being loose with definitions here, as I've written "100" and "10" using the very system I'm trying to define. Feel to replace with tally marks: 2*10 is ‖*卌卌.

As you can see, functions are integral parts of any notation. So when I start turning to new notations by using functions to describe them, you shouldn't act as though this is somehow fundamentally different from the notations that you likely already use in everyday life. Using Knuth arrow notation is no less valid for saying a number's name than writing "123". They're both just names that point at a specific number of tally marks.

Defining Operations

Let's start with addition. Addition is an operation, not a number. But it's easier to talk in terms of operations when you get to really big numbers, so I want to start here. We'll begin with a first approximation of a really big number: 123. In terms of addition, you might say it is 100+23, or maybe 61+62. Or you may want to break it down to its tally marks: 卌卌卌…卌⦀. This is all quite unwieldy, though. I'd prefer to save space when typing all this out. So let's instead use the relatively small example of 9, not 123. You might not think of 9 as a really big number, but we've only just started. The first function, F₁(x,y), involves taking the numeral X and doing whatever operation it is Y times. In this series of functions, I'm always going to use 3 for both x and y to make things as simple as possible. F₁ is addition, so F₁(3,3)=3+3+3=9.

Each subsequent function Fₓ is just a repetition of the previous function. Addition is repeated counting, but when you repeat addition, that's just multiplication. So our second operation, multiplication, can be looked at as F₂=3*3*3=27.

(As an aside, a similar function to Fₓ(3,2) can be seen at the On-Line Encyclopedia of Integer Sequences. Their a(n) is equivalent to our Fₓ(3,2), where x=n-1. So their a(2) is our F₁(3,2). You may also notice that F₂(3,2)=F₁(3,3),  so although the OEIS sequence A054871 is out of sync on the inputs, the series nevertheless matches what we're discussing here.)

I want to pause here to point out that multiplication grows more quickly than addition. Look at the first few terms of F₁:

• F₁(3,1)=3
• F₁(3,2)=3+3=6
• F₁(3,3)=3+3+3=9

Then compare to the first few terms of F₂:

• F₂(3,1)=3
• F₂(3,2)=3*3=9
• F₂(3,3)=3*3*3=27

What's important here isn't that 27>9. What's important is that the latter function is growing more quickly than the previous one.
We can keep going to F₃, which uses the exponentiation operation. This is as high as most high school math classes go. F₃=3^3^3=19683. The first few terms of F₃ are:

• F₃(3,1)=3
• F₃(3,2)=3^3=27
• F₃(3,3)=3^3^3=19683

You can see that each subsequent function is growing more and more quickly, such that the only the third term, Fₓ(3,3), is fast approaching really big numbers.

Next in the series is F₄, which uses tetration. F₄=3⇈3⇈3=7,625,597,484,987. Here I am using Knuth arrow notation for the operator symbol, but the idea is the same as all the previous operations. Addition is repeated counting. Multiplication is repeated addition. Exponentiation is repeated multiplication. Tetration is repeated exponentiation. In other words:

• Multiplication is repeated addition:
  X*Y = X+X+…+X, where there are Y instances of X in this series.
  In the case of F₂(3,2), 3*3=3+3+3.
• Exponentiation is repeated multiplication:
  X^Y = X*X*…*X, where there are Y Xs.
  3^3=3*3*3
• Tetration is repeated exponentiation:
  X⇈Y = X^X^…^X, where there are Y Xs.
  3⇈3=3^3^3

Pentation is next: F₅=3↑↑↑3↑↑↑3. It takes a bit of work to figure out this value in simpler terms.

• F₅=3↑↑↑3↑↑↑3
  =3↑↑↑(3↑↑↑3)
  =3↑↑↑(3⇈3⇈3)
  =3↑↑↑(3⇈(3⇈3))
  =3↑↑↑(3⇈(7,625,597,484,987))

Remember that tetration is repeated exponentiation, so the part in the parentheses there (3⇈7,625,597,484,987) is 3 raised to the 3 raised to the 3 raised to the 3…raised to the 3, where there are 7,625,597,484,987 instances of 3 in this power tower. The image to the right shows what I mean by a power tower: it's a^a^…^a. In our example, it's 3^3^…^3, with 7,625,597,484,987 threes. And this is just the part in the parentheses. You still have to take 3↑↑↑(N), where N is the huge power tower of threes. It's truly difficult to accurately describe just how big this number truly is.

Fastly Fast

So far I've described the first few functions, F₁, F₂, F₃, F₄, and F₅. These are each associated with an operation. I could go on from pentation to hexation, but instead I want to focus on these increasingly fast growing functions. F₅(3,3) is already mindboggingly huge, so it's difficult to get across how huge F₆(3,3) is in comparison. Think about the speed at which we get to huge numbers from F₁ to F₂ to F₃, and then realize that this is nothing compared to where you get when you move to F₄. And again how this is absolutely and completely dwarfed by F₅. This happens yet again at F₆. It's not just much bigger. It's not just bigger than F₅ by the hugeness of F₅. It's not twice as big, or 100 times as big, nor even F₅ times as big. (After all, the word "times" denotes puny multiplication.) It's not F₅^F₅ even. Nor F₅⇈F₅. Nor even F₅↑↑↑F₅. No, F₆=3⇈⇈3⇈⇈3=3⇈⇈(F₅(3,3)). I literally cannot stress how freakishly massive this number is. And yet: it is just F₆.

This is why I wanted to focus on fast growing functions. Each subsequent function is MUCH bigger than the last, in such a way that the previous number basically approximates to zero. So imagine the size of the numbers as we move along to faster and faster growing functions.

These functions grow fast because they use recursion. Each subsequent function is doing what the last function did, but does it repeatedly. In our case, Fₓ(3,3) is just taking the previous value and using the next highest operator on it. F₂(3,3)=3*F₁(3,3). F₃(3,3)=3^F₂(3,3). F₄(3,3)=3⇈F₃(3,3). F₅(3,3)=3↑↑↑F₄(3,3). And as we saw two paragraphs ago, F₆(3,3)=3⇈⇈F₅(3,3).

I chose this recursive series of functions because I wanted to match up with the examples I used in my previous discussion of really big numbers. But most mathematicians use the fast growing hierarchy to describe this kind of thing. Think of it as a yardstick against which we can compare other fast growing functions.

Fast Growing Hierarchy

We start with F₀(n)=n+1. This is a new function, unrelated to the multiple input function we've used earlier in this blog post. F₀(n) is the first rung of the fast growing hierarchy. If you want to consider a specific number associated with each rung of the hierarchy, we might choose n=3. So F₀(3)=3+1=4.

We then use recursion to define each subsequent function in the hierarchy. Fₓ₊₁(n)=Fₓ(Fₓ(…Fₓ(n)…)), where there are n instances of Fₓ.

So F₁(n)=F₀(F₀(…F₀(n)…)), with n F₀s. This is equivalent to n+1+1+…+1, where there are n 1s. This means F₁(n)=n+n=2n. In our example, F₁(3)=6.

Next is F₂(n)=F₁(F₁(…F₁(n)…)), with n F₁s. This is just 2*2*…*2*n, with n 2s. So F₂(n)=n2^n. In our example, F₂(3)=3*(2^3)=24.

At each step in the hierarchy, we roughly increase to the next level of operation each time. F₀ is basically addition; F₁ is multiplication; F₂ is exponentiation. It's not exact, but it's in the same ballpark. This corresponds closely to the function I defined earlier in this blog post. Mathematicians use the fast growing hierarchy to give an estimate of how big other functions are. My F₂(3,3) from earlier is roughly F₂(n) in the FGH. (F₂(3,3)=27, while F₂(3)=24.) (Egads, do I regret using F for both functions, even though it should be clear since one has multiple inputs.)

Diagonalization

So at this point you probably get the gist of the fast growing hierarchy for F₂, F₃, F₆, etc. Even though they are mind-boggingly large numbers, you may be able to grasp what we mean we talk about F₉, or F₉₉. These functions grow faster and faster as you go along the series of functions, and there's an infinite number of functions in the list. We can talk about Fₓ with the subscript x being a googol, or 3↑↑↑3↑↑↑3. These functions grow fast. But we can do even better.

Let's define F𝜔(n) as Fn(n). (Forgive the lack of subscripts here; we're about to get complex on what's down there.) Now our input n is going to be used not just as the input in the function, but also as the FGH rank of a function that we already defined above. So, in our example, F𝜔(3)=F₃(3)=F₂(F₂(F₂(3)))=F₂(F₂(24))=F₂(24(2^24))=F₂(24(16777216))=F₂(402653184)= 402653184*(2^402653184)≈10^120000000.

As you can see, F𝜔(n) grows incredibly quickly. More quickly, in fact, than any integer value of Fₓ(n). This means that the sequence of functions I've been talking about previously in this blog post can't even get close to the fast growing F𝜔(n), even though there are infinite integer values you could plug in for Fₓ. An example of a famous function that grows at this level would be the Ackermann function.

But we can keep going. Consider F𝜔₊₁(n), which is defined exactly as we defined the FGH earlier. F𝜔₊₁(n)=F𝜔(F𝜔(…F𝜔(n)…)), where there are n F𝜔s. This grows faster than F𝜔(n) in a way that is exceedingly difficult to describe. Remember that each function in this sequence grows so much faster than the previous function so as to make it approximate zero for a given input. An example of a famous function that grows at this level would be Graham's function, of which Graham's number is oft cited as a particularly large number. In particular, F𝜔₊₁(64)>G₆₄.

There's no reason to stop now. We can do F𝜔₊₂(n) or F𝜔₊₆(n) or, in general, F𝜔₊ₐ(n), where a can be any natural number, as high as you might please. You can use a=googol or a=3↑↑↑3↑↑↑3 or even a=F𝜔(3↑↑↑3↑↑↑3). But none of these would be as large as if we introduced a new definition: F𝜔*₂(n)=F𝜔₊n(n). This is defined in exactly the same way that we originally defined F𝜔(n), where the input not only goes into the function, but also into the FGH rank of the function itself. F𝜔*₂(n) grows even faster than any F𝜔₊ₐ(n), regardless of what value you enter in as a.

I'm sure you see by now where this is going. We have F𝜔*₂₊₁(n) next, and so on and so forth, until we get F𝜔*₂₊ₐ(n), with an arbitrarily large a. Then we diagonalize again to get F𝜔*₃(n), and then the family of F𝜔*₃₊ₐ(n). This can on indefinitely, until we get to F𝜔*ₑ₊ₐ(n), where e can be arbitrarily large. A further diagonalization can then be used to create F𝜔*𝜔(n)=F𝜔²(n), which grows faster than F𝜔*ₑ₊ₐ(n) for any combination of e and a.

Yet F𝜔²(n) isn't a stopping point for us. Beyond F𝜔²₊₁(n) lies F𝜔²₊ₐ(n), beyond which is F𝜔²₊𝜔(n), beyond which is the F𝜔²₊𝜔₊ₐ(n) family, and so on, and so forth, past 𝜔²₊𝜔*₂(n), beyond 𝜔²₊𝜔*ₑ₊ₐ(n), all the way to F𝜔³(n). At each step, the functions grow so fast that they completely and utterly dwarf the function before it, and yet we've counted up several times to infinity in this sequence, an infinite number of times, and then did this three times in order to get to F𝜔³(n). These functions grow fast.

Still, there's more to consider. F𝜔³(n) is followed by F𝜔⁴(n), all the way up to F𝜔ⁿ(n), beyond which lies yet another digonalization to get to F𝜔^𝜔(n). From here, you can just redo all the above: F𝜔^𝜔₊ₐ(n) to F𝜔^𝜔₊𝜔₊ₐ(n) to F𝜔^𝜔₊₂𝜔₊ₐ(n) to F𝜔^𝜔₊ₑ𝜔₊ₐ(n) until we have to rediagonalize to F𝜔⇈𝜔(n), which we set equal to Fₑ₀(n) just for the purpose of making it easier to read. There are two famous examples of functions that grow at this level of the FGH: the function G(n) = "the length of the Goodstein sequence starting from n" and the function H(n) = "the maximum length of any Kirby-Paris hydra game starting from a hydra with n heads" are both at the FGH rank of Fₑ₀(n).

You can keep going, obviously. Tetration isn't the end for 𝜔. We can do Fₑ₀₊₁(n), then the whole family of Fₑ₀₊ₐ(n), followed by Fₑ₁(n). And we can keep going, to Fₑ₂(n) and beyond, increasing the exponent arbitrarily large, followed by Fₑ𝜔(n). And this ride just doesn't stop, because you go through the whole infinite sequence of infinite sequences of infinite sequences of infinite sequences of infinite sequences yet again, increasing the subscript of e to the absurd point of ε₀. And then we can repeat that, and repeat again, and again, infinitely many times, creating a subscript tower where ε has a subscript of ε to the subscript of ε to the subscript of ε to the suscript of… -- infinitely many times. At this point the notation gets too unwieldy yet again, so we move on to using another greek letter: 𝛇, where it starts all over again. And we can do this infinite recursion infinitely yet again, until we have a subscript tower of 𝛇s, after which we can call the next function in the series η.

Each Greek letter represents an absolutely humongous jump, from 𝜔 to ε to 𝛇 to η. But as you can see it gets increasingly complicated to talk about these FGH functions. Enter the Veblen Hierarchy.

Veblen Hierarchy

The Veblen Hierarchy starts with 𝜙₀(a)=𝜔^a, then increases with each subscript to a new greek letter from before. So:

• 𝜙₀(a)=𝜔^a
• 𝜙₁(a)= ε^a
• 𝜙₂(a)= 𝛇^a
• 𝜙₃(a)= η^a

This FGH grows much faster than the previous one, because it skips over all the infinite recursions to the final tetration of each greek letter, which it defines as the next greek letter in the series. The Veblen Hierarchy grows fast.

The subscript can get bigger and bigger, reaching 𝜙ₑ(a), where e is arbitrarily large. You can follow this by making 𝜔 the next subscript in the series, then follow the same recursive expansion as before until you get to 𝜔⇈𝜔, which we'd define as ε. And go through the greek letters, one by one, until you've gone through an infinite number of them, after which we can use 𝜙 as the subscript for 𝜙. Then do this again and again, nesting additional 𝜙 as the subscript for each 𝜙, until you have an infinite subscript tower of 𝜙, after which you have to substitute a new notation: Γ₀.

Here we finally reach a new limit. Γ₀ is as far as you can go by using recursion and diagonalization. It's the point at which we've recursed as much as we can recurse, and diagonalized as much as we can diagonalize. 

But we can go further.

We can already see Γ₀ as 𝜙(a,0)=a. Let's extend Veblen function notation by defining 𝜙(1,0,0)=γ₀. Adding this extra variable let's us go beyond all the recursion and diagonalization we could do previously. Now we have all of that, and can just add 1.

Let's explore this sequence:

• γ₀=𝜙(1,0,0) Start here.
• γ₁=𝜙(1,0,1) Increment the last digit repeatedly.
• γ_𝜔=𝜙(1,0,𝜔) Eventually you reach 𝜔.

After this, the next ordinal is 𝜙(1,1,0). As you can see, we have a new variable to work with. We can keep incrementing the right digit until we get to 𝜔 again, after which we reach 𝜙(1,2,0). And we can do this again and again, until we reach 𝜙(1,𝜔,0). Then the next ordinal would be 𝜙(2,0,0). And we can keep going, more and more until we get to 𝜙(𝜔,𝜔,𝜔). At this point, we're stuck again.

That is, until we add an additional variable.

So now we have 𝜙(1,0,0,0) as the next ordinal. And we can max this out again until we need to add yet another variable, and then yet another variable, and so on, until we have infinite variables. This is called the Small Veblen Ordinal.

ψ(ΩΩω)=φ(1,0,⋯,0⏟ω)

Among FGH functions, the Small Veblen Ordinal ranks in just the lower attic of Cantor's Attic. It's not even the fastest growing function on the page it's listed on. We're nowhere near the top, despite all this work. Of course, there isn't a top -- not really. But what I mean is that we're nowhere near the top of what mathematicians talk about when they work with really large ordinals.

…and Beyond!

You might notice that at no point did I mention TREE(3), which was one of the numbers I brought up in my last blog post. That's because the TREE() function is way beyond what I've written here. You have to keep climbing, adding new ways of getting to faster and faster growing functions before you reach anything like TREE(3). And beyond that to the point of absurdity is SSCG(3). And these are all still vastly beneath the Church Kleene Ordinal, which (despite being countable) is uncomputable. This is where you finally run into the Busy Beaver function. The distances between each of these functions that I've mentioned in this paragraph are absurdly long. It took this long to explain up to the Small Veblen Ordinal, and yet it would take equally long to get up to the TREE() function. And then just as long to get to SSCG(). And just as long to Busy Beaver.

I want to be clear: I'm not saying they are equal distances from each other. I'm saying that it would take an equal amount of time to explain them. At each step of my explanation, I've gotten to absurdly faster and faster growing functions, leaping from concept to concept more quickly than I had any right to. And I would explain that much faster if I kept going, using shorthand to handwave away huge jumps in logic. And yet it would still take that long to explain up to these points.

And I still wouldn't even be out of the lower attic, with the Church Kleene Ordinal.

If you want to keep going, you may be interested in this readable medium post by Josh Kerr, the absolutely beautifully written Who Can Name the Bigger Number? by Scott Aaronson, or the wiki at Cantor's Attic. Parts of this post were inspired by my own previous post on large numbers and a reddit post by PersonUsingAComputer. I'd also like to thank professor Edgar Bering and grad students Bo Waggoner and Charlie Cunningham for helping to correct errors in this essay.