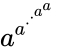R(5,5)

I was told today that the number 45 was ruined by Trump. I found this difficult to parse at first — to me, a number is not ruined just because it has an association with something bad. But I think that there is more to it than just that. The weather service predicts rain as she'll come home from work today. As the day started (just after midnight here), Russia began an invasion of Ukraine. It really isn't the greatest start to Katherine's 45th birthday for several reasons. (And she was so looking forward to any day that represented a multiple of 5, her favorite number.)

At first, I pointed out Grover Cleveland. Sure, Trump is widely said to be the "45th" president. But since Cleveland was both the 22nd and 24th president (being elected both just prior to and immediately after the little-talked-about Benjamin Harrison), that means that Trump is only the 44th person to take on the mantle of the presidency overall.

Then, to bolster my claim, I remember the old claim that one person was President temporarily. David Rice Atchison has a plaque affixed to a statue in Plattsburg, Missouri, which states: "President of United States One Day". This refers to March 4, 1849, when he was chosen as president pro tempore in the Senate where he resided. The Senate's own website tells the rest of the story:

> On March 2, 1849, Vice President George M. Dallas took leave of the Senate for the remainder of the session and the Senate elected Atchison as president pro tempore. ... Until the adoption of the Twentieth Amendment in 1933, presidential and congressional terms began and ended at noon on March 4. In 1849 March 4 fell on a Sunday. On the morning of March 4, President James Polk signed the last of the session’s legislation at the White House and at 6:30 a.m. recorded in his diary, “Thus closed my official term as President.” The Senate, having been in session all night, adjourned sine die at 7:00 a.m. President-elect Zachary Taylor, in observance of the Christian Sabbath, preferred not to conduct his inauguration on Sunday, March 4, and the ceremony was delayed until the next day. On Monday, March 5, Taylor took the oath of office on the Capitol’s east front portico and the transition of power was complete.

> But if President Polk’s term ended on March 4 at noon, and Zachary Taylor was not sworn in until noon on March 5, who was president on March 4? Under the Presidential Succession Act of 1792 the Senate president pro tempore immediately followed the vice president in the line of presidential succession. Had Atchison been president from noon on March 4 to noon on March 5?

If the answer is yes, then, I at first thought, that might save the number 45. But then I realized that, if Athison had indeed served as president, then that would again make Trump the 45th person to take the role, since Cleveland served twice!

Thankfully, the answer is no. But I'm starting to suspect that this won't appease someone who feels that 45 is ruined anyway.

What, then, can rehabilitate 45? In the eyes of someone who loves the number 5, a strong contender is the fact that 45 is the conjectured value of the Ramsey number R(5,5). What is the least number number of guests that you must invite in order to ensure that at least five guests will know each other or at least five guests will not? Mathematicians are not sure, but we suspect it is 45.

To be slightly more general, R(m,n) gives an answer to the question of the least number of guests you'd need to invite in order to ensure that at least m guests know each other, or that at least n guests don't know each other. R(5,5) is known to be between 43 and 49 inclusive, and is conjectured to be 45. (See OEIS entry A120414 on Conjectured Ramsey Numbers R(n,n).) (To be even more general, R(m,n) refers to the idea that "complete disorder is impossible"; given a sufficiently large set, order will appear among its proper subsets. This is the first basic finding in Ramsey theory, which focuses on order amid disorder.)

Figuring out these numbers are deceptively difficult. Joel Spencer writes about Paul Erdős quip: if aliens come and demand to know the value of R(5,5) or they will destroy Earth, we should marshal all of our computers and mathematicians in an attempt to find the value. But if they demand to know R(6,6), we're better off attempting to destroy the aliens. In fact, Ramsey numbers appear to be difficult to calculate even with hypothetical quantum computers.

If 5 is a great number, and the most exciting parts of mathematics are the parts that lie just on our horizon, and if finding order within disorder is one of the enjoyable parts of being an artist, then R(5,5) must be a special case of representing something that might make up for Trump's taint. While we can't guarantee that it is 45 (some suspect 43 instead), it stands out as something that should make Katherine's 45th birthday special.

Happy birthday, Katherine. <3

I'll close with a poem by Ernest Davis entitled The Ramsey Number R(5,5):

There are fans, among math buffs, of e and of π.
The ratio golden has legions who sigh,
In reverent awe at its beauty ideal.
Euler's γ has got its own quirky appeal.
But what makes me feel tingly, aroused, and alive
Is the mystical integer R(5,5). [Read "R of five five"]

Like Batman and Robin, its everyday face
Is a secret identity quite commonplace.
It's an integer, experts on graph theory state,
At least 43 and at most 48.
And combinatorists laboriously strive
To narrow the bounds known for R(5,5).

It's a quite element'ry idea to define
(Though I don't want to try that in meter and rhyme).
A short, simple program in Python or C
Has no trouble at all finding R(3,3)
But the stars in the sky will no longer survive
Ere it prints out the value of R(5,5).

Said Erdos: "If aliens from far outer space
Want to know, or they'll wipe out the whole human race
If we join all our forces, perhaps we'll contrive
To tell them the value of R(5,5).
But we'll certainly be in a hell of a fix
If they ask for the value of R(6,6)."

A Valentine's Day Card

Giving something meaningful each Valentine's Day has become a sort of tradition between Katherine and myself.

This year, Katherine has truly outdone herself. Her handmade card quotes Carl Sagan's Demon-Haunted World, showcasing a principle that has guided my life ever since I first became a skeptic some twenty odd years ago. It's a principle that I've held close to my being and that has been at the heart of many conversations Katherine and I have about so many different things. She writes that the balance between openness to new ideas and ruthless skepticism is a dance where each of us often switch sides in our cooperative search for truth. Alongside the quote, she has made literal pinpricks of light, referencing the lone lights in the darkness that rational thinking helps us to uncover. These represent the deep truths that lie within the deep nonsense — the very same deep truths that we slowly aim to uncover as we dig through the arguments about the problems of our time.

Upon opening the card, we see that there is yet another layer to the quote on the cover. She says that I brighten her life, implying that, at a different level, the darkness of the card itself also represents our lives, separated, and the lights we have managed to uncover are the shining moments we have made in the course of our relationship. All of this is said within the confines of a Sierpinski triangle, a fractal shape of crystalline regularity that reveals yet another layer of meaning: here, the balance is in the construction of the shape, with its open spaces throughout (literally it has an area of 0) and the numerous lights that we nevertheless uncover via the application of strict logical rules within the triangle itself. It is a saga that shows us the things we can count on even within a field where nothing can be counted on. Here, she implies, is where our love resides.

On yet another layer of interpretation, we see that the lights themselves overwhelm the structure of the sierpinski triangle. The triangle itself is drawn in a dark color that is difficult to see on the black background even with the lights turned off — once they are turned on, it becomes impossible to see the logical order belying them. Only the front of the card, written in reflective ink, remains visible to the human eye when the lights wash out the scene on the dark void itself. Yet even then it is a difficult thing to make out: you must struggle to see the path before you. Ironically, it is the brightness of the lights, not the darkness of the background, that makes this so difficult. This, again, is in reference to our relationship: so many of our brightest moments sometimes overshadow our typical moments in life, and make it that much more difficult to see the structure beneath it all when we reside day by day.

I am completely taken aback at the various layers of meaning weaved into a single card. So many of our conversations over the past years point back to many of the points made on the card itself. I am sure that, to any other person, this must look just like a black card with lights embedded within. But, to me, I see the threads of our relationship here: the discussions and presented arguments, the successes within a background of seeming impossibility, and the simple joys that overwhelm even the lowest of lows in a relationship of this magnitude.

I don't know how I can top this, but I will have to up my game next year.

See also the Puzzle Portraiture she made for me, the screen print of The Tuft of Flowers, & her drawing of Jasper and the Amiibo. You can see more of her work at KatherineHess.com.

Cubic Star Number

Katherine's latest art project involves looking at the number of covid cases in our county every other day and making something that has to do with that number. On Monday of this week, there were 2140 cases per 100,000 residents in Montgomery County (averaged over the previous seven days). Katherine discovered that this was a "cubic star number", which she felt had an interesting name, but for which there was not a good explanation online. (Seriously, try looking it up yourself. No one seems to have ever written about it much at all (other than the A051673 OEIS sequence), and there certainly aren't any pictures of what the accompanying shape would look like.)

While making a three dimensional sculpture out of 2140 elements would be a little much for a series where she makes a new piece of art every other day, it did seem reasonable to make a much smaller cubic star number shape out of 120 marbles. So she did.

What you're seeing here is (as far as I can tell) the first picture of a cubic star number searchable on the internet. While diagrams of these may exist in yet-to-be-indexed books, I could not find such a picture in anything that refers to cubic star numbers (such as Gulliver's 2002 article Sequences from Arrays of Integers).

Star numbers are relatively well known. They're centered figurate numbers: you take one dot, then surround it with more dots in a certain shape, then surround that with dots, and so on, until you have a big shape of dots with a central dot in the middle. Gamers might recognize that a Chinese checkers board uses a star number shape of 121 spaces.

The star number polygon shown here consists of a hexagon with triangles on each side (i.e., a hexagram). But you don't have to use a hexagon on the inside. You could just as easily use a square, with four triangles on each side of that square. This square star number might not look as pleasing as the hexagram does, but it has interesting properties all on its own.

But I think things get even more interesting once you move into the third dimension. Instead of a square, you can use a cube; and, rather than making a stellated shape where a pyramid exists on every face of the square, you can merely place the pyramids on four of the sides, so that the front and back of the cube remain flat. In this way, you're extrapolating out what a two dimensional star number might look like if you literally pulled it out into a new dimension, but turned the triangles into pyramids while allowing the square to fill out a cube.

Almost no one talks about cubic star numbers. The closest I could find was a blogger referencing house numbers, which, to be fair, has a more distinctive shape to them. House numbers are closely related to cubic star numbers; rather than four pyramids, they exhibit just one. But it's easy to see how you can get to a cubic star number from the corresponding house number: just add three more pyramids and stick 'em on the sides.

Katherine chose to use the fourth cubic star number, 120. It consists of a 4x4x4 cube with four pyramids that each have a 3x3 base. This small cubic star number was created entirely out of marbles, using liquid silicone to connect them. It stands as a symbol of the much larger tenth cubic star number, 2140, which consists of a 10x10x10 cube with four pyramids that each have a 9x9 base.

I'm fascinated by Katherine's choices in what to display in this regular art series. COVID-19 has gotten pretty bad here in Montgomery County, Maryland, since the Omicron strain took over. We reached highs of 300 cases on this graph back in 2020, and that was scary because anything above 100 was considered high and worthy of shutting down schools. Now we hover in the ~2k range and people are demanding that schools remain open. She's dealing with the strain via creating art — I have to admit that that's better than my current method of shutting down nearly entirely.

I'm looking forward to seeing what else Katherine comes up with. I was fascinated by her prime factorization series, and this current series on the integers of covid cases seems just as good. I just wish we didn't have to keep spreading covid in order to generate these depressing numbers and associated fascinating art.

Cubic Star Number

Exploring the Integer of Seven Day Average Covid Cases per 100,000 People in my County Series. On Monday, January 10,...

Posted by Katherine Hess on Wednesday, January 12, 2022

On the surreality of .999 repeating...

When I was in grade school, I often had late evening talks with my friend, Peter. Topics of discussion varied wildly from day to day, sometimes about video games like Doom, sometimes about girls, and sometimes about math. On one specific evening, we talked about infinitely small numbers.

I think the topic held our attention because the books we had access to said, in no uncertain terms, that the decimal expansion .9̅ is equivalent to 1. This left no room for a smaller value, in between .9̅ and 1, but which nevertheless was distinct from 1. We found this perplexing, as there seemed to be nothing logically incoherent with the idea of having an infinitely small positive value which we could subtract from 1 — yet the textbooks made it clear that that resulting difference could not be .9̅, since .9̅=1.

This idea is not unique. Many people make the same error, thinking that .9̅ should be strictly less than 1. In the sci.math newsgroup, the main FAQ's top entry for decades showed that .9̅=1. When I took a look at sci.math just now in November 2021, one of the most recent entries is literally someone making the argument that they are distinct. This is a topic that gets brought up again and again, and there's always someone more knowledgeable around that works tirelessly to correct these misunderstandings. (I used to be that guy on the old skeptic forums, though thankfully not on math ones.)

But in order to tread new frontiers in mathematics, you sometimes have to take a "yes, and..." approach. Sometimes when you do so, you're able to reach new ground that later ends up bearing significant fruit. This is how it was with negative numbers, this is how it was with imaginary numbers, and maybe something similar could be said with the idea of a positive number so small that even adding an infinite number of them together will not sum up to 1.

I first discovered the concepts in Berlekamp, Conway, and Guy's Winning Ways for Your Mathematical Plays back when I was working my way through Feynman's Lectures on Physics. I had been gifted a very nice three volume set as a teenager, and while the first book wasn't terribly difficult to get through, I was having trouble understanding books 2 and 3. At the time, I had dropped out of school, and so my only way to read these Feynman lectures required me to first teach myself more complex mathematics. I went to the local library, taking out texts that would help me to get through what Feynman had written, and, occasionally, I'd use the internet to supplement my understanding. Back then we did not have 3Blue1Brown; the best online math explainers were merely paragraphs of html text alongside slowly loading jpgs. So it was hard going. Nevertheless, I kept at it and eventually learned what I needed in order to properly enjoy my boxed set of Feynman lectures.

Hackenbush girl from WWfYMP.

It was during one of these online math excursions that I came across Andy Walker's excellent late 1990s-era html maths-explainer: Hackenstrings, and the .999?=1 FAQ. Walker walks us through a simplified version of Conway's Hackenbush idea, showing the beginnings of what we now call surreal numbers. Here, Conway and Knuth take seriously the idea that there could be a positive number so small that adding it to itself infinitely many times would never add up to any traditional real number. This is the first time that an infinitesimal is taken seriously enough to warrant the creation of a new system of numbers. (At least it's the first time since limits replaced infinitesimals in our teaching of calculus.)

At the time, I was too immature to think that I should purchase for myself Winning Ways for Your Mathematical Plays, but I ever so much wish that I had. It's an amazing book and well worth the read.

If you're interested in learning more, I highly recommend this excellent video by Owen Maitzen that does an absolutely amazing job of explaining Hackenbush. While it's an hour long, this is nevertheless one of the most entertaining introductions to a new type of math that I've seen anyone on the internet create. (He's even composed a soundtrack that suits his video perfectly!) Well done, Owen.

Honoring Petrov Day by NOT Pressing the Button

Thirty-eight years ago, Stanislav Petrov disobeyed orders that may have caused a nuclear attack. I'll quote from Yudkowsky's retelling of Petrov's story:

On September 26th, 1983, Lieutenant Colonel Stanislav Yevgrafovich Petrov was the officer on duty when the warning system reported a US missile launch.  Petrov kept calm, suspecting a computer error.

Then the system reported another US missile launch.

And another, and another, and another. 

What had actually happened, investigators later determined, was sunlight on high-altitude clouds aligning with the satellite view on a US missile base.

In the command post there were beeping signals, flashing lights, and officers screaming at people to remain calm.  According to several accounts I've read, there was a large flashing screen from the automated computer system saying simply "START"….

Petrov decided that, all else being equal, he would prefer not to destroy the world.  He sent messages declaring the launch detection a false alarm, based solely on his personal belief that the US did not seem likely to start an attack using only five missiles.

Petrov was first congratulated, then extensively interrogated, then reprimanded for failing to follow procedure.  He resigned in poor health from the military several months later.

Each year, I and many others take a moment to think back to the day when the world as we know it almost died. Of all the traditions I follow, this is perhaps the most solemn. (In 2018, I attended a ceremony where the Future of Life Institute posthumously presented Stanislav Petrov the $50,000 Future of Life Award.)

From Petrov Day 2020.

This year, I have been invited to take part in an experiment of mutually assured destruction. LessWrong and the Effective Altruism Forum have decided to honor Petrov day by creating buttons on each site which, if pressed with the appropriate arming code, will take the other site down for the duration of the day. I was chosen by the EA Forum as one of the people trusted with the launch codes capable of taking down LessWrong's site.

To outsiders, this exercise may seem silly. It has the appearance of a mere game, but I think it is much more than that: it is a serious ritual, one where the stakes involve thousands of visitors to each site, one where defection will be public, one where we practice the very real act of not causing wanton destruction due to mistrust, carelessness, or flippancy. But yes, it is also a game: one with stakes we should not callously risk.

Last year, this experiment failed. LessWrong user Chris Leong pressed the button, taking down the site during Petrov Day 2020. The failure, I believe, was not entirely on his part, but also due to a poor choice of who would be entrusted with the launch codes. I am hopeful that the decision to trust me with the codes this year will not be in vain.

At the same time, I am cognizant that the concept of mutually assured destruction here is supposed to incentivize the other team to not press their button. This presents a dilemma to me: I honestly do not want to press a button that will take down LessWrong's site. But should I keep open the possibility, should LessWrong press their button to take down the EA Forum? In order for the threat of MAD to work, I must precommit to taking an action that might not make sense in the moment when I have to take it. But I abhor the idea of precommitting myself to such an action.

Homepage of the EA Forum today.

I'm not going to strike first. That much is certain. But I'm less sure about my stance on a retaliatory strike. I want to say that even if they fire first, I will not fire back. What use is there in additional destruction? But this intellectually seems like the wrong stance to take. This exercise is repeated each year; Tit for Tat does seem like the better policy. That requires precommitting to MAD. At the same time, I don't take precommitting to anything lightly.

So here I stake my claim: if the EA Forum goes down due to LessWrong pressing their button, I may press in retaliation. This is not an idle threat. I do think that I may press, just to ensure that future Petrov days don't undergo the same terrible defection. But I'm not precommitting. Hopefully, LessWrong will understand this to be a credible threat, even if not entirely likely. I am hopeful that this small amount of threat will be sufficient to prevent them from deciding to press their button.

(If you are reading this on Petrov Day, Sept 26, after 11 a.m. ET, you can see the button on LessWrong and the EA Forum's home pages if they are still up. Or, if one side has already defected, you will see that the other side's site will be taken down.)

38 years ago, Stanislav Petrov saved the world. This year, I was chosen by @EAForumPosts as steward of codes that can take down https://t.co/FKbNMjxAxI for a day. Meanwhile LW holds codes for https://t.co/eWAOaSiIdl. I hope nothing happens this Petrov Day. https://t.co/RlXOyBQwc1

— Eric Herboso (@EricHerboso) September 26, 2021

38 years ago, Stanislav Petrov saved the world. This year, I was chosen by the Effective Altruism Forum as steward of...

Posted by Eric Herboso on Sunday, September 26, 2021

Most Functions with Predictive Power in the Natural Sciences are Non-Differentiable

Epistemic status: highly uncertain.

Recently, Spencer Greenberg posted three useful facts about mathematics:

Here's the most useful mathematics I can fit in 3 short paragraphs (see image). pic.twitter.com/DM2ytwelYo

— Spencer Greenberg 🔍 (@SpencrGreenberg) December 5, 2020

This generated a bit of discussion on facebook:

Here's the most useful mathematics I can fit in 3 short paragraphs (see image). -- Note: each week, I send out One...

Posted by Spencer Greenberg on Friday, December 4, 2020

In one of the comment threads, I put forward what I thought to be an uncontroversial thought: that although it is true that most useful mathematics in the natural sciences are differentiable, this is not because the useful math stuff happens to also be differentiable, but instead because we can (mostly) only make sense of the differentiable stuff, so that's the stuff that we find useful. This is a weak anthropic argument that merely makes the statement partially vacuous. (It's like saying I, who reads only English, find that most useful philosophy to me is written in English. It's true, but not because there is a deep relationship between useful philosophy and it being written in English.)

It turns out that this was not considered an uncontroversial thought:

However, I also received a number of replies that indicated that I did a poor job of explaining my position in facebook comments. (And I wanted to ensure that I wasn't making some critical mistake in my thinking after hearing so many capable others dismiss the idea outright.) To fix this, I decided to organize my thoughts here. Please keep in mind that I'm not certain about the second section on math in the natural sciences at all (although I think the first section on pure math is accurate), and in fact I think that, on balance, I'm probably wrong about this essay's ultimate argument. But whereas my confidence level is maybe around 20% for this line of thinking, I'm finding that others are dismissing it completely out of hand, and so I find myself arguing for its validity, even if I personally doubt its truth. (In the face of uncertainty, we need not take a final position (unless it's moral uncertainty), but we should at least understand other positions enough to steelman them.)

Mathematics Encompasses More Than We Can Know

Before we talk about the natural sciences, let's look at something simpler: really big numbers. When it comes to counting numbers, it's relatively easy to think of big ones. But, unless you're a math person, you may not fully comprehend just how big they can get. It's easy to say that the counting numbers go on forever, and that they eventually become so large that it becomes impossible to write them down. Yet it's actually stranger than that: they eventually get to be so big that they can't be thought of (except expressed in this way). As a simple example, consider that there exists a least big whole number such that it can't, even in principle, be thought of by a human being. Graham's number, for example, is big enough that if you were somehow able to hold the base ten version of it in your brain, the sheer amount of information held would mean that your brain would quite literally implode. Yet we can still talk about it; I just did earlier, when I called it Graham's number. The thing is: the counting numbers keep going, so eventually you can reach a number so high that its informational content cannot be expressed without exceeding the maximum amount of entropy that the observable universe can hold.

Opening one's eyes to this helps with the following realization: not all numbers are nameable. Somehow, despite being an amateur interested in math for most of my life, having thought I understood Cantor's diagonal argument after reading through it several times, teaching it to others several times, and talking about it several times, I recently learned that I had skipped understanding something basic about it that wasn't made clear to me before:

Cantor's diagonal proof shows that we can't enumerate all the reals. Wrong!(?) What Cantor really shows is only that there can’t be an enumeration of all the reals of our mathematical universe. It only refers to the merely countably many nameable reals! https://t.co/LH3tN6kjiv

— Eric Herboso (@EricHerboso) November 15, 2020

Scott Aaronson's excellent explanation on this really hits home. The parts of the number line that we can name are but countable dust among the vast majority of points that we have no way of writing down in any systematic way. We can only vaguely point toward them when making mathematical arguments and can only really make basic (unappended) statements that either apply to zero, one, or an infinite amount of them at once. We can, for example, say that a random real number picked between 0 and 1 has certain properties, but if we try to say which number it is, we must use some kind of systematic method to point it out, like 1/3 = 0.3 repeating.

Something similar is true when it comes to functions. Most functions, by far, are not nameable. They are relations between sets that don't follow any pattern that makes sense to humans. For a finite example, consider the set X:{a,b,c} as a domain and Y:{d,e,f} as the range. We can construct a function f()that maps X➝Y in pretty much any way we please. Each function we create this way is nameable, but only because it is finite. Imagine instead doing this for an infinite field, with each input going to a random output. Out of all possible functions mapping ℝ to itself, almost none are continuous, and thus almost none are differentiable. Almost all of them are not even constructable in any systematic way. They are, ultimately, not really understandable by us humans right now, which is why we don't really have people doing math work on those topics at all.

Mathematics in the Natural Sciences

So far, we've established that, in pure mathematics at least, the vast majority of functions are not understandable by humans today. Thankfully, we understand a lot about differentiable functions (and some others that are easily constructable, like additions of multiple different differentiable functions separated by kinks, stepwise functions, &c.). As has been pointed out previously, the natural world uses differentiable functions all over the place. Modern physics is awash with these types of functions, and they all do an extraordinary job, giving us an amazing amount of predictive power across the spectrum from the very large to the very small. Nothing in what I'm about to say can take anything away from that in the least.

But it occurs to me that although it is uncontestedly true that almost all the useful-to-us functions governing the natural world around us are also differentiable functions, it may be that this is true for anthropic reasons, not because of some underlying feature of ultimately-useful-functions-in-the-natural-sciences themselves.

I'm not at all sure that this would actually be true, but it doesn't seem to contradict anything I know if to suppose that there may be a great many functions governing the natural world that aren't differentiable, and that the only reason we don't use them in the natural sciences is because we can't currently understand them. They are uncountable dust, opaque to us, even if, one day, our understanding of mathematics and natural science improves enough so that may eventually use these functions to make predictions in just the same way that we currently use differentiable functions. In short: the reason why almost all useful functions are differentiable is because we really only can usefully read differentiable functions. It is not (necessarily) that the useful functions in the natural world all happen to be differentiable.

Ockham's Razor

One counterargument given to me in the facebook thread involves Ockham's razor:

They are saying that while there may be no reason that this supposition might be true, we shouldn't think that it is true because, by Ockham's razor, we should prefer the hypothesis that doesn't include these extra not-yet-discovered non-differentiable functions that have predictive power over the natural world.

Before I respond to this, I feel that I have to first look more closely at what Ockham's razor actually does. I'll quote myself from Why Many Worlds is Correct:

The law of parsimony does not refer to complexity in the same way that we use the word in common usage. Most of the time, things are called "complex" if they have a bunch of stuff in them, and "simple" if they have relatively less stuff. But this cannot possibly be what Occam's razor is referring to, since we all gladly admit that Occam's Razor does not imply that the existence of multiple galaxies is less likely to be true than just the existence of the Milky Way alone.

Instead, the complexity referred to in Occam's razor has to do with the number of independent rules in the system. Once Hubble measured the distance to cepheid variables in other galaxies, physicists had to choose between a model where the laws of physics continue as before and a model where they added a new law saying Hubble's cepheid variables measurements don't apply. Obviously, the model with the fewer number of physical laws was preferable, given that both models fit the data.

Just because a theory introduces more objects says nothing about its complexity. All that matters is its ruleset. Occam's razor has two widely accepted formulations, neither of which care about how many objects a model posits.

Solomonoff inductive inference does it by defining a "possible program space" and giving preference to the shortest program that predicts observed data. Minimum message length improves the formalism by including both the data and the code in a message, and preferring the shortest message. Either way, what matters is the number of rules in the system, not the the number of objects those rules imply.

What's relevant here is that while it is true that this argument is introducing vast new entities in the form of currently ununderstandable functions that may have predictive power, it is not introducing a new rule in doing so. Those ununderstandable functions certainly do exist; they're just not studied because studying them wouldn't be useful. So the question is: does saying that they might have predictive power introduce a new hypothesis? Or does it make more sense to say that of course some of them have predictive power; we just can't use them to predict things because we don't understand those functions. If the former, then Ockham's razor would act against this supposition; if the latter, then Ockham's razor would act against those who would claim that these functions can't have predictive power.

It's unclear to me which of these is the case. I don't want to play reference class tennis about this, but the latter certainly feels true to me. The analogous Borges' Library of Babel certainly shows that an infinite number of these non-differentiable real-world functions will have predictive power (though maybe not explanatory power?), but this isn't sufficient to say that MOST functions with predictive power are non-differentiable. I think that probably most functions with predictive power are in fact differentiable -- but I'm not at all certain about this, and that's why I'm arguing for that side. I think that others are wrong to so quickly dismiss the idea that most functions with predictive power might be non-differentiable. They're probably correct in thinking that it's wrong, but the certainty with which they think it is wrong seems very off to me. Hopefully, after reading this blog post you might agree.

edit on 10 December 2020: Neural Nets

Originally I ended this blog post with the previous paragraph, but Ben West points out that neural nets have a black box that uses functions very like what I've described to make actual real-world predictions:

My confidence in this idea has increased upon realizing that there already exist at least some functions for which we do not know if they are differentiable or not that definitely have predictive power. It's important to point out that it's still possible that this thesis is wrong; it may be the the black box functions that neural nets find are all differentiable, and, in fact, that even still seems likely to me, but I definitely now give more credence to the idea that some might not be.

Fastly Fast Growing Functions

In a previous post, I discussed Really Big Numbers, moving from many children's example of a big number, a million, up past what most people I meet would think of as a huge number, a googol, and ultimately going through Graham's number, TREE(3), the busy beaver function, infinities and beyond. I wasn't aware of it at the time, but a much better version of that post already existed: Who Can Name the Bigger Number?, by Scott Aaronson.

In my original post, I made a few errors in the section about fast growing functions. Some kind commentors helped correct the most egregious errors, but the ensuing corrections littered that entire section of the post with strikethrough text that I was never really happy with. Now, six years later, I'd like to finally make up for my mistakes.

The Goal

I'd like to name some really, really big numbers. I'm not going to talk about the smaller ones, nor the ones that delve into infinities; you can read the previous post for that. Here I just want to point toward some really big finite numbers. The numbers I'm aiming for are counting numbers, like 1, 2, or a billion. They're not infinite in size. These are numbers where, if someone asked you to write a really, really big number, these would be way beyond what the questioner was thinking of, and yet still wouldn't be infinite in extent.

Why Functions?

We always use functions when writing numbers. It's just that most of the time, it's invisible to us. If we're counting apples, we might make a hatch mark (or tally mark) for the first apple, another hatch for the second ("‖"), and so on. This works fine for up to a dozen apples or so, but it starts to get pretty difficult to understand at a glance. You might fix this by making every fifth hatch cross over the previous four ("卌"), but you quickly run into a problem again if you get too many sets of five hatch marks.

It's easier to come up with a better notation, like using numerals. Now we can use "1" or "5", rather than actually write out all those hatch marks. Then we can use a simple function to make our notation easier to follow. The rightmost numeral is the ones place, then next to the left is the tens place, and the next to the left is the hundreds place, and so on. So "123" means (1*100)+(2*10)+(3*1). Of course, I'm being loose with definitions here, as I've written "100" and "10" using the very system I'm trying to define. Feel to replace with tally marks: 2*10 is ‖*卌卌.

As you can see, functions are integral parts of any notation. So when I start turning to new notations by using functions to describe them, you shouldn't act as though this is somehow fundamentally different from the notations that you likely already use in everyday life. Using Knuth arrow notation is no less valid for saying a number's name than writing "123". They're both just names that point at a specific number of tally marks.

Defining Operations

Let's start with addition. Addition is an operation, not a number. But it's easier to talk in terms of operations when you get to really big numbers, so I want to start here. We'll begin with a first approximation of a really big number: 123. In terms of addition, you might say it is 100+23, or maybe 61+62. Or you may want to break it down to its tally marks: 卌卌卌…卌⦀. This is all quite unwieldy, though. I'd prefer to save space when typing all this out. So let's instead use the relatively small example of 9, not 123. You might not think of 9 as a really big number, but we've only just started. The first function, F₁(x,y), involves taking the numeral X and doing whatever operation it is Y times. In this series of functions, I'm always going to use 3 for both x and y to make things as simple as possible. F₁ is addition, so F₁(3,3)=3+3+3=9.

Each subsequent function Fₓ is just a repetition of the previous function. Addition is repeated counting, but when you repeat addition, that's just multiplication. So our second operation, multiplication, can be looked at as F₂=3*3*3=27.

(As an aside, a similar function to Fₓ(3,2) can be seen at the On-Line Encyclopedia of Integer Sequences. Their a(n) is equivalent to our Fₓ(3,2), where x=n-1. So their a(2) is our F₁(3,2). You may also notice that F₂(3,2)=F₁(3,3),  so although the OEIS sequence A054871 is out of sync on the inputs, the series nevertheless matches what we're discussing here.)

I want to pause here to point out that multiplication grows more quickly than addition. Look at the first few terms of F₁:

• F₁(3,1)=3
• F₁(3,2)=3+3=6
• F₁(3,3)=3+3+3=9

Then compare to the first few terms of F₂:

• F₂(3,1)=3
• F₂(3,2)=3*3=9
• F₂(3,3)=3*3*3=27

What's important here isn't that 27>9. What's important is that the latter function is growing more quickly than the previous one.
We can keep going to F₃, which uses the exponentiation operation. This is as high as most high school math classes go. F₃=3^3^3=19683. The first few terms of F₃ are:

• F₃(3,1)=3
• F₃(3,2)=3^3=27
• F₃(3,3)=3^3^3=19683

You can see that each subsequent function is growing more and more quickly, such that the only the third term, Fₓ(3,3), is fast approaching really big numbers.

Next in the series is F₄, which uses tetration. F₄=3⇈3⇈3=7,625,597,484,987. Here I am using Knuth arrow notation for the operator symbol, but the idea is the same as all the previous operations. Addition is repeated counting. Multiplication is repeated addition. Exponentiation is repeated multiplication. Tetration is repeated exponentiation. In other words:

• Multiplication is repeated addition:
  X*Y = X+X+…+X, where there are Y instances of X in this series.
  In the case of F₂(3,2), 3*3=3+3+3.
• Exponentiation is repeated multiplication:
  X^Y = X*X*…*X, where there are Y Xs.
  3^3=3*3*3
• Tetration is repeated exponentiation:
  X⇈Y = X^X^…^X, where there are Y Xs.
  3⇈3=3^3^3

Pentation is next: F₅=3↑↑↑3↑↑↑3. It takes a bit of work to figure out this value in simpler terms.

• F₅=3↑↑↑3↑↑↑3
  =3↑↑↑(3↑↑↑3)
  =3↑↑↑(3⇈3⇈3)
  =3↑↑↑(3⇈(3⇈3))
  =3↑↑↑(3⇈(7,625,597,484,987))

Remember that tetration is repeated exponentiation, so the part in the parentheses there (3⇈7,625,597,484,987) is 3 raised to the 3 raised to the 3 raised to the 3…raised to the 3, where there are 7,625,597,484,987 instances of 3 in this power tower. The image to the right shows what I mean by a power tower: it's a^a^…^a. In our example, it's 3^3^…^3, with 7,625,597,484,987 threes. And this is just the part in the parentheses. You still have to take 3↑↑↑(N), where N is the huge power tower of threes. It's truly difficult to accurately describe just how big this number truly is.

Fastly Fast

So far I've described the first few functions, F₁, F₂, F₃, F₄, and F₅. These are each associated with an operation. I could go on from pentation to hexation, but instead I want to focus on these increasingly fast growing functions. F₅(3,3) is already mindboggingly huge, so it's difficult to get across how huge F₆(3,3) is in comparison. Think about the speed at which we get to huge numbers from F₁ to F₂ to F₃, and then realize that this is nothing compared to where you get when you move to F₄. And again how this is absolutely and completely dwarfed by F₅. This happens yet again at F₆. It's not just much bigger. It's not just bigger than F₅ by the hugeness of F₅. It's not twice as big, or 100 times as big, nor even F₅ times as big. (After all, the word "times" denotes puny multiplication.) It's not F₅^F₅ even. Nor F₅⇈F₅. Nor even F₅↑↑↑F₅. No, F₆=3⇈⇈3⇈⇈3=3⇈⇈(F₅(3,3)). I literally cannot stress how freakishly massive this number is. And yet: it is just F₆.

This is why I wanted to focus on fast growing functions. Each subsequent function is MUCH bigger than the last, in such a way that the previous number basically approximates to zero. So imagine the size of the numbers as we move along to faster and faster growing functions.

These functions grow fast because they use recursion. Each subsequent function is doing what the last function did, but does it repeatedly. In our case, Fₓ(3,3) is just taking the previous value and using the next highest operator on it. F₂(3,3)=3*F₁(3,3). F₃(3,3)=3^F₂(3,3). F₄(3,3)=3⇈F₃(3,3). F₅(3,3)=3↑↑↑F₄(3,3). And as we saw two paragraphs ago, F₆(3,3)=3⇈⇈F₅(3,3).

I chose this recursive series of functions because I wanted to match up with the examples I used in my previous discussion of really big numbers. But most mathematicians use the fast growing hierarchy to describe this kind of thing. Think of it as a yardstick against which we can compare other fast growing functions.

Fast Growing Hierarchy

We start with F₀(n)=n+1. This is a new function, unrelated to the multiple input function we've used earlier in this blog post. F₀(n) is the first rung of the fast growing hierarchy. If you want to consider a specific number associated with each rung of the hierarchy, we might choose n=3. So F₀(3)=3+1=4.

We then use recursion to define each subsequent function in the hierarchy. Fₓ₊₁(n)=Fₓ(Fₓ(…Fₓ(n)…)), where there are n instances of Fₓ.

So F₁(n)=F₀(F₀(…F₀(n)…)), with n F₀s. This is equivalent to n+1+1+…+1, where there are n 1s. This means F₁(n)=n+n=2n. In our example, F₁(3)=6.

Next is F₂(n)=F₁(F₁(…F₁(n)…)), with n F₁s. This is just 2*2*…*2*n, with n 2s. So F₂(n)=n2^n. In our example, F₂(3)=3*(2^3)=24.

At each step in the hierarchy, we roughly increase to the next level of operation each time. F₀ is basically addition; F₁ is multiplication; F₂ is exponentiation. It's not exact, but it's in the same ballpark. This corresponds closely to the function I defined earlier in this blog post. Mathematicians use the fast growing hierarchy to give an estimate of how big other functions are. My F₂(3,3) from earlier is roughly F₂(n) in the FGH. (F₂(3,3)=27, while F₂(3)=24.) (Egads, do I regret using F for both functions, even though it should be clear since one has multiple inputs.)

Diagonalization

So at this point you probably get the gist of the fast growing hierarchy for F₂, F₃, F₆, etc. Even though they are mind-boggingly large numbers, you may be able to grasp what we mean we talk about F₉, or F₉₉. These functions grow faster and faster as you go along the series of functions, and there's an infinite number of functions in the list. We can talk about Fₓ with the subscript x being a googol, or 3↑↑↑3↑↑↑3. These functions grow fast. But we can do even better.

Let's define F𝜔(n) as Fn(n). (Forgive the lack of subscripts here; we're about to get complex on what's down there.) Now our input n is going to be used not just as the input in the function, but also as the FGH rank of a function that we already defined above. So, in our example, F𝜔(3)=F₃(3)=F₂(F₂(F₂(3)))=F₂(F₂(24))=F₂(24(2^24))=F₂(24(16777216))=F₂(402653184)= 402653184*(2^402653184)≈10^120000000.

As you can see, F𝜔(n) grows incredibly quickly. More quickly, in fact, than any integer value of Fₓ(n). This means that the sequence of functions I've been talking about previously in this blog post can't even get close to the fast growing F𝜔(n), even though there are infinite integer values you could plug in for Fₓ. An example of a famous function that grows at this level would be the Ackermann function.

But we can keep going. Consider F𝜔₊₁(n), which is defined exactly as we defined the FGH earlier. F𝜔₊₁(n)=F𝜔(F𝜔(…F𝜔(n)…)), where there are n F𝜔s. This grows faster than F𝜔(n) in a way that is exceedingly difficult to describe. Remember that each function in this sequence grows so much faster than the previous function so as to make it approximate zero for a given input. An example of a famous function that grows at this level would be Graham's function, of which Graham's number is oft cited as a particularly large number. In particular, F𝜔₊₁(64)>G₆₄.

There's no reason to stop now. We can do F𝜔₊₂(n) or F𝜔₊₆(n) or, in general, F𝜔₊ₐ(n), where a can be any natural number, as high as you might please. You can use a=googol or a=3↑↑↑3↑↑↑3 or even a=F𝜔(3↑↑↑3↑↑↑3). But none of these would be as large as if we introduced a new definition: F𝜔*₂(n)=F𝜔₊n(n). This is defined in exactly the same way that we originally defined F𝜔(n), where the input not only goes into the function, but also into the FGH rank of the function itself. F𝜔*₂(n) grows even faster than any F𝜔₊ₐ(n), regardless of what value you enter in as a.

I'm sure you see by now where this is going. We have F𝜔*₂₊₁(n) next, and so on and so forth, until we get F𝜔*₂₊ₐ(n), with an arbitrarily large a. Then we diagonalize again to get F𝜔*₃(n), and then the family of F𝜔*₃₊ₐ(n). This can on indefinitely, until we get to F𝜔*ₑ₊ₐ(n), where e can be arbitrarily large. A further diagonalization can then be used to create F𝜔*𝜔(n)=F𝜔²(n), which grows faster than F𝜔*ₑ₊ₐ(n) for any combination of e and a.

Yet F𝜔²(n) isn't a stopping point for us. Beyond F𝜔²₊₁(n) lies F𝜔²₊ₐ(n), beyond which is F𝜔²₊𝜔(n), beyond which is the F𝜔²₊𝜔₊ₐ(n) family, and so on, and so forth, past 𝜔²₊𝜔*₂(n), beyond 𝜔²₊𝜔*ₑ₊ₐ(n), all the way to F𝜔³(n). At each step, the functions grow so fast that they completely and utterly dwarf the function before it, and yet we've counted up several times to infinity in this sequence, an infinite number of times, and then did this three times in order to get to F𝜔³(n). These functions grow fast.

Still, there's more to consider. F𝜔³(n) is followed by F𝜔⁴(n), all the way up to F𝜔ⁿ(n), beyond which lies yet another digonalization to get to F𝜔^𝜔(n). From here, you can just redo all the above: F𝜔^𝜔₊ₐ(n) to F𝜔^𝜔₊𝜔₊ₐ(n) to F𝜔^𝜔₊₂𝜔₊ₐ(n) to F𝜔^𝜔₊ₑ𝜔₊ₐ(n) until we have to rediagonalize to F𝜔⇈𝜔(n), which we set equal to Fₑ₀(n) just for the purpose of making it easier to read. There are two famous examples of functions that grow at this level of the FGH: the function G(n) = "the length of the Goodstein sequence starting from n" and the function H(n) = "the maximum length of any Kirby-Paris hydra game starting from a hydra with n heads" are both at the FGH rank of Fₑ₀(n).

You can keep going, obviously. Tetration isn't the end for 𝜔. We can do Fₑ₀₊₁(n), then the whole family of Fₑ₀₊ₐ(n), followed by Fₑ₁(n). And we can keep going, to Fₑ₂(n) and beyond, increasing the exponent arbitrarily large, followed by Fₑ𝜔(n). And this ride just doesn't stop, because you go through the whole infinite sequence of infinite sequences of infinite sequences of infinite sequences of infinite sequences yet again, increasing the subscript of e to the absurd point of ε₀. And then we can repeat that, and repeat again, and again, infinitely many times, creating a subscript tower where ε has a subscript of ε to the subscript of ε to the subscript of ε to the suscript of… -- infinitely many times. At this point the notation gets too unwieldy yet again, so we move on to using another greek letter: 𝛇, where it starts all over again. And we can do this infinite recursion infinitely yet again, until we have a subscript tower of 𝛇s, after which we can call the next function in the series η.

Each Greek letter represents an absolutely humongous jump, from 𝜔 to ε to 𝛇 to η. But as you can see it gets increasingly complicated to talk about these FGH functions. Enter the Veblen Hierarchy.

Veblen Hierarchy

The Veblen Hierarchy starts with 𝜙₀(a)=𝜔^a, then increases with each subscript to a new greek letter from before. So:

• 𝜙₀(a)=𝜔^a
• 𝜙₁(a)= ε^a
• 𝜙₂(a)= 𝛇^a
• 𝜙₃(a)= η^a

This FGH grows much faster than the previous one, because it skips over all the infinite recursions to the final tetration of each greek letter, which it defines as the next greek letter in the series. The Veblen Hierarchy grows fast.

The subscript can get bigger and bigger, reaching 𝜙ₑ(a), where e is arbitrarily large. You can follow this by making 𝜔 the next subscript in the series, then follow the same recursive expansion as before until you get to 𝜔⇈𝜔, which we'd define as ε. And go through the greek letters, one by one, until you've gone through an infinite number of them, after which we can use 𝜙 as the subscript for 𝜙. Then do this again and again, nesting additional 𝜙 as the subscript for each 𝜙, until you have an infinite subscript tower of 𝜙, after which you have to substitute a new notation: Γ₀.

Here we finally reach a new limit. Γ₀ is as far as you can go by using recursion and diagonalization. It's the point at which we've recursed as much as we can recurse, and diagonalized as much as we can diagonalize. 

But we can go further.

We can already see Γ₀ as 𝜙(a,0)=a. Let's extend Veblen function notation by defining 𝜙(1,0,0)=γ₀. Adding this extra variable let's us go beyond all the recursion and diagonalization we could do previously. Now we have all of that, and can just add 1.

Let's explore this sequence:

• γ₀=𝜙(1,0,0) Start here.
• γ₁=𝜙(1,0,1) Increment the last digit repeatedly.
• γ_𝜔=𝜙(1,0,𝜔) Eventually you reach 𝜔.

After this, the next ordinal is 𝜙(1,1,0). As you can see, we have a new variable to work with. We can keep incrementing the right digit until we get to 𝜔 again, after which we reach 𝜙(1,2,0). And we can do this again and again, until we reach 𝜙(1,𝜔,0). Then the next ordinal would be 𝜙(2,0,0). And we can keep going, more and more until we get to 𝜙(𝜔,𝜔,𝜔). At this point, we're stuck again.

That is, until we add an additional variable.

So now we have 𝜙(1,0,0,0) as the next ordinal. And we can max this out again until we need to add yet another variable, and then yet another variable, and so on, until we have infinite variables. This is called the Small Veblen Ordinal.

ψ(ΩΩω)=φ(1,0,⋯,0⏟ω)

Among FGH functions, the Small Veblen Ordinal ranks in just the lower attic of Cantor's Attic. It's not even the fastest growing function on the page it's listed on. We're nowhere near the top, despite all this work. Of course, there isn't a top -- not really. But what I mean is that we're nowhere near the top of what mathematicians talk about when they work with really large ordinals.

…and Beyond!

You might notice that at no point did I mention TREE(3), which was one of the numbers I brought up in my last blog post. That's because the TREE() function is way beyond what I've written here. You have to keep climbing, adding new ways of getting to faster and faster growing functions before you reach anything like TREE(3). And beyond that to the point of absurdity is SSCG(3). And these are all still vastly beneath the Church Kleene Ordinal, which (despite being countable) is uncomputable. This is where you finally run into the Busy Beaver function. The distances between each of these functions that I've mentioned in this paragraph are absurdly long. It took this long to explain up to the Small Veblen Ordinal, and yet it would take equally long to get up to the TREE() function. And then just as long to get to SSCG(). And just as long to Busy Beaver.

I want to be clear: I'm not saying they are equal distances from each other. I'm saying that it would take an equal amount of time to explain them. At each step of my explanation, I've gotten to absurdly faster and faster growing functions, leaping from concept to concept more quickly than I had any right to. And I would explain that much faster if I kept going, using shorthand to handwave away huge jumps in logic. And yet it would still take that long to explain up to these points.

And I still wouldn't even be out of the lower attic, with the Church Kleene Ordinal.

If you want to keep going, you may be interested in this readable medium post by Josh Kerr, the absolutely beautifully written Who Can Name the Bigger Number? by Scott Aaronson, or the wiki at Cantor's Attic. Parts of this post were inspired by my own previous post on large numbers and a reddit post by PersonUsingAComputer. I'd also like to thank professor Edgar Bering and grad students Bo Waggoner and Charlie Cunningham for helping to correct errors in this essay.

Effective Advertising and Animal Charity Evaluators

This entry was originally posted on Effective-Altruism.com. It is reposted here for reference only.

[Summary: Animal Charity Evaluators wants to address feedback that we've heard from the effective altruism community regarding our online marketing practices. Although we follow best practices in the advertising industry, some EAs feel that we sometimes use advertising which glosses over details and is potentially misleading to the public. As the communications data scientist for ACE, I explain why we feel these advertising practices are not only net beneficial to the EA community, but also should not be considered to be misleading.]

Our mission at ACE is to find and promote the most effective ways to help animals. One of the ways in which the promotion part of our mission is fulfilled most effectively is through reaching those who are most passionate about helping animals but who have not yet been introduced to the concept of effective altruism.

While some of our ads are aimed at existing EAs, the majority of our advertising efforts focus on the above audience for three reasons: (1) the large scale of this audience compared with the size of the EA audience, (2) our belief that they have the most potential for change once they learn about effective animal advocacy (EAA), and (3) the fact that their counterfactual donations seem likely to be less impactful than those of EAs.

We have received some feedback on a few of these marketing practices—specifically, we have received feedback suggesting that we might not be advertising in a way that the EA community would most like to see. I will go over a few such examples before sharing why we use our current methods of advertising.

Double Donations

In late 2017, we held a donation-matching campaign. A generous donor offered to match any donations we received to the ACE Recommended Charity Fund. This Fund is not used for ACE operations; the entirety of this Fund goes toward our recommended charities. (We now have a checkbox indicating that users may choose to donate 10% of their gift directly to ACE, but at the time we had already reached our funding cap for the year and were not accepting new donations.)

We know that the EA community is generally not in favor of donation-matching campaigns. There are four main reasons why this is so:

1. Most donation-matching campaigns are illusory
2. Non-illusory campaigns may do harm via double-counting
3. Matching campaigns encourage dishonesty
4. There may be better ways for large donors to leverage their money

Most donation-matching campaigns are illusory

At ACE, we are careful to ensure that any matching campaigns are entirely non-illusory. GiveWell has pointed out several problems with illusory matching campaigns. We agree with their reasoning. For example, last year a donor approached us asking about doing a matching campaign to benefit ACE; we declined it because their donation was going to happen whether we set up a campaign or not.

However, not all matching campaigns are illusory. For our year-end donation-matching campaign in 2017, we had a donor who would not otherwise have given to our Recommended Charity Fund but who was interested in doing a donation-matching campaign with us. We discussed how a non-illusory campaign might very likely reach a broader audience, inspiring hundreds of new people to participate in effective giving for the first time. We believe this type of influence matching is especially effective with non-EAs. However, as Karnofsky points out, it may be better for existing EAs to ignore the influence matching aspect when making decisions on where to donate—even if we prefer non-EAs to be influenced by them.

ACE’s commitment to non-illusory matching campaigns alleviates the concern raised by Jeff Kaufman about counterfactual trust and contradicts the assumptions made by most polled EAs on Facebook. Sometimes even illusory donation-matching campaigns can be beneficial (as Avi Norowitz points out with the Facebook #GivingTuesday retrospective) but this requires special circumstances.

We are careful to explicitly note our position on these influence-matching campaigns in our FAQ, and we believe that using them has been a net positive for our non-EA audience.

Non-illusory campaigns may cause harm via double-counting.

Ben Hoffman has rightfully pointed out that overassignment of credit can obscure opportunity costs with donation-matching campaigns. Given two rational EA actors, believing that each is causing the other to donate may result in a scenario where each is giving less optimally than they’d otherwise choose. However, this example only causes harm if both sides are changing their mind on where to donate due to the existence of the donation match.

At ACE, we only accept matching campaigns where this does not occur. While we don’t have full certainty of their counterfactual actions, we believe our matching donor not only would likely have counterfactually given a smaller amount elsewhere had we not done the campaign (thus making our campaign non-illusory), but also that they would have counterfactually funded a different non-EAA donation-matching campaign. This ensures that, at most, only one side is influenced by the matching campaign—and so evades the situation Hoffman describes where double-counting causes harm.¹

Matching campaigns encourage dishonesty

Overassigning credit isn’t the only way that matching campaign incentives reward dishonesty. In 2016 Benjamin Todd reported that 80,000 Hours had previously run partially counterfactually valid donation matching campaigns, by allowing the donor to commit to delaying funding rather than ensuring that the funding is completely counterfactually valid. Ben Kuhn ran a survey that found that most donors expect matching campaigns to be entirely counterfactually valid, so this remains an issue.

At ACE, we’ve tried to maintain a balance of being intellectually honest and using copywriting that isn’t overly wordy. During our year-end donation-matching campaign, we initially used advertisements that contained the phrase “Double Your Impact”, but then switched to “Double Your Donation” after receiving feedback about where that balance made the most sense.²

We believe using “Double Your Donation” as an advertisement headline strikes that balance well. It is an appropriate shorthand for what is actually occuring: the amount of money that would go to this fund was indeed doubled, and, had the donation match not occurred, our matching donor may have given to a different non-EA cause.

As further evidence that these are real counterfactual matches where influenced donations are legitimately doubled, in 2016 and 2017 we surpassed the agreement of what the donor had originally offered to match, after which the donor followed up by continuing the match through these additional donations to more than double what they originally offered toward the matching challenge.

There may be better ways for large donors to leverage their money

Ben Kuhn performed a survey of research on the effectiveness of matching campaigns, concluding that matching campaign effects are generally smaller than we might at first expect, and suggesting that there are more effective ways for large donors to leverage their money. We have no reason to doubt the validity of his analysis, though we do have limited conflicting anecdotal data from our matching campaigns.

When we are approached by large donors, we generally try to steer them away from the donation-matching campaigns they are ordinarily used to, advising them to fund general unrestricted programs and administration instead. However, last year we set a funding cap for our own operations; once met, there are only so many other ways that large donors can leverage their money. When a legitimate influence-matching campaign opportunity arises, we don’t think it is inappropriate to take advantage of it at the 1:1 rate, even if the returns may not be as much as you might expect.

Anecdotally, we’ve found that our matching campaigns have brought in a disproportionately large number of new donors—the majority of whom were not previously involved with effective giving. While we did not set up a control group, we can report that 73% of the donors to our 2017 matching campaign were first-time donors with ACE, and our post-donation survey showed that over 80% of respondents reported being motivated to give specifically due to the matching opportunity. In addition to the hundreds of thousands of dollars raised by this new audience,³ we were able to teach them about effective animal advocacy and to support them in effective giving elsewhere in the EA movement. The amount that these donors will give to effective charities during their lifetime is significantly higher than the donation-matching campaign that attracted them; we continue to build relationships with these new donors. So while we concur with Kuhn that the raw donation amounts might not be as influenced by a donation match as we may at first think, in our case the flow-through effects seem to more than make up for this difference.

Utilons Versus Fuzzies

Another advertising example that has received some limited criticism from the EA community is our tendency to use cute pictures of animals and catchy messaging in many of our ads. We’ve heard this critique several times in person at EA conferences, although it’s rare to see the argument explicitly laid out online. The idea is that advertising in a way that tugs at people’s fuzzies may be appropriate for direct-level EAA organizations such as The Humane League, but that a meta-charity like ACE should focus solely on arguments for maximizing utility. By posting cute pictures or clever one-liners, we may be misrepresenting the type of work we do. After all, GiveWell’s Facebook feed rarely uses pictures other than to show graphs or their logo; and MIRI’s feed focuses on showcasing data, not cute pictures.

We feel that these lines of argumentation misunderstand the role that ACE plays in the EA movement. Yes, we have a core audience of EAs who use our charity recommendations—and yes, those recommendations are based on what we find to be most effective. We fully identify as an effective altruist organization. However, a large portion of our intended audience is comprised of animal lovers who are not yet aware of EA principles. We strongly believe that this is the audience that is capable of making the largest positive change once they learn about effective animal advocacy. Catching their attention via cute animal pictures is the best way we’ve found so far to get them to read more about why effectiveness is important.

We have data to support this. We’ve experimented with pushing out various types of Facebook posts to both our current audience (to increase engagement) and to potential new followers. Although we make a point to post a combination of EA-oriented messaging alongside posts that showcase cute animals, the only posts that receive traction significant enough to generate engagement and reach a larger audience are the ones that use fuzzies, not utilons, as the main hook.

Facebook in particular has a positive feedback loop where the posts which garner the most reactions and engagement tend to be shown to more followers, whereas the lower-performing posts only get shown to a subset of our Facebook audience. This results in the average Facebook user getting the impression that the majority of our posts are fuzzies-centric on trending topics, when in reality a considerable amount of our posts are utility-centric on data-oriented news.⁴

This feedback loop works to our advantage. Over time, the best performing posts reach non-EA audiences who are likely to be sympathetic to the cause of effective animal advocacy. This allows our brand to grow consistently, introducing new people to the ideas of the EA movement.

Graph Accuracy and Completeness

We’re currently in the process of improving some of our graphs in order to make them more easily shareable. For example, our donation impact page includes a violin plot that shows how many animals we estimate are spared by a $1,000 donation. While the data is accurate, the resulting graph is very difficult to interpret—and is therefore not ideal for sharing at animal rights conferences or on social or journalistic media. The amount of time it takes to explain probability density to passersby at non-EA conferences or to general online audiences looking for a quick picture that explains ACE’s thoughts usually exceeds their (understandably limited) attention span. If we want to reach these audiences, we need to produce graphs that illustrate the point much more efficiently.

However, sharing just the average estimates (seven animals spared for shelters and 4,056 for ACE recommended charities) could be seen as deceitful, as it doesn’t take into account the uncertainty involved in making these calculations.⁵ Clearly, there is some compromise between a full violin plot and sharing just the mean as the best single estimate for each category. We are still working out where that balance lies.

A similar issue comes up with our donation allocation chart.⁶ The data on the left omits wild fishes, who receive almost no portion of animal charity donations. The data on the left also includes animals used for clothing, but the data on the right replaces that category with “mixed or other activities.” On the page, we explicitly point out how the “mixed or other” category was put together, giving an example of guide dog training as one component. This matters because some advocates may consider subcategories like guide dog training as a primarily human-centric charity, not an animal charity, and this might affect the relative size of the chart regions. However, when this chart does gets shared online, it’s generally just the image portion that people will copy and paste. Although these shared images will not include the surrounding text, we believe it is sufficient to include the extra information on our website. We feel similarly with regard to the analogous donation impact chart; including the probability densities as additional information on our site is sufficient, so long as the chart itself includes ranges for our cost-effectiveness estimates.

Marketing Best Practices

The above marketing practices are specific to EA organizations. Most non-EA organizations do not object to setting up illusory donation-matching campaigns, nor reaching out based on fuzzies, nor ensuring that graphics are as accurate as possible. We care about these issues because we are committed to the norm of being extraordinarily honest.⁷ As Ben Hoffman rightly points out, “When the activity of extracting money from donors is abstracted away from…other core activities of an organization…, best practices tend towards distorting the truth.”

This doesn’t mean we should shy away from all nonprofit marketing best practices. To the extent that we can reach out to new audiences, increase the number of donors who are giving effectively, and grow our brand without compromising what we believe in, we feel that using best practices is both acceptable and desirable.

One of our goals is to continually be better able to introduce non-EA animal advocates to effective animal advocacy ideas. We accomplish this through several methods:

• We try to speak in language that non-EA animal advocates already understand when in an appropriate context. This not only means using cute pictures in social media posts, but also talking about projects and interventions that may not be a currently understood top intervention, so long as it reasonably could apply.
• We use multivariate testing on social media adverts and email campaigns, but we are careful to only test messaging that matches our brand and to only use subject lines that accurately convey the content of each email.
• We segment our audience, showing different information to different audiences, while being careful not to cut information sent to various audiences in a way that might be seen as deceitful. Specifically, we take care to only show different content based on the different interests of our audience; we do not alter the meaning behind our messages when segmenting our audience.
• We use a Google ad grant and SEO efforts to gain traffic from audiences not yet familiar with effective animal advocacy, without deceiving visitors as to what they will see once they visit.
• We track key performance indicators to judge how effective our communications strategies perform, but are careful not to focus on quantity at the expense of quality.
• We create videos that appeal to a general audience through fuzzies in addition to posting videos of webinars and symposium talks.
• We take advantage of opportunities to direct more funding to effective animal charities, such as running a non-illusory matching campaign that is very likely to inspire new people to give effectively.

While we are careful not to blindly follow marketing best practices, we nevertheless utilize them when they don’t interfere with our values. We prize integrity and take care to exhibit norms of honesty when following accepted marketing principles. We do not use “rhetorical tricks” nor “sales techniques” to convince others; our use of imagery is solely used to gain attention. Arguments for EAA on our site are fully transparent, and we both accept and encourage feedback on the research we perform.

I’m proud to report that we are continuing to grow our brand, increase the number of donors who are giving effectively, and introduce new audiences to effective animal advocacy. In December last year, we raised over $1.26 million for our Recommended Charity Fund⁸—a significant portion of which came from extremely generous first-time donors not already identifying themselves as EAs. Of course, we couldn’t achieve these results for our recommended charities without the support of EAs, who so generously helped to fully fund ACE directly last year, but the larger point is that these strategies are encouraging non-EAAs to donate to more effective causes and are making a subset more aware of effective altruism in general.

If you work with an EA organization, we would love to hear about the marketing/communications techniques and/or successes that you’ve had when promoting EA organizations. We’d also like to hear if anyone has any concerns about ACE or any other EA charity using these kinds of marketing techniques. Are you comfortable with ACE’s methods of using donation-matching campaigns? Do you agree that marketing with fuzzies is acceptable even for a charity evaluator like ACE? What’s the minimal amount of information our shareable images should convey?⁹ Do you feel that the way ACE follows nonprofit marketing best practices is appropriate?

We look forward to hearing your thoughts.

---

¹ This donor decided to give to our Recommended Charity Fund on the basis of our recommendation, not by calculating the additional effects of the matching campaign, because they counterfactually would have done a different donation-matching campaign anyway. This means that while an overassignment of credit may have occurred, this overassignment did not change how the donor would have counterfactually acted. ↩

² In November 2017 we initially used the phrase “This means that you can double the impact of your donation from now through the end of the year by donating to our Recommended Charity Fund” in at least one marketing material, but after receiving feedback from both ACE staff members and outside EAs (including Remmelt Ellen and Marianne van der Werf—thank you to both!) we standardized to the “double your donation” language instead across all marketing materials.

In previous years we were less strict about our language, using “Double Your Impact” in several advertisements during the 2015 and 2016 giving seasons. We did not make this choice blindly; at the time, we felt that “double your impact” and “double your donation” were different mostly in what kinds of audiences they attract, and that this overrode any concerns about one being more strictly accurate than the other. “Double your impact” emphasizes the effect of helping others, whereas “double your donation” emphasizes what one can personally accomplish.

Note that these terms are regularly used interchangeably in fundraising campaigns outside the EA community, and we then felt that most people wouldn’t take campaign headlines literally. In 2017, we updated to believing that it was not enough for our FAQ to describe our commitment to non-illusory matching campaigns, and we standardized to only use “double your donation” language going forward. ↩

³ New donors made up 56% of the pre-matched amount raised during our 2017 matching campaign. ↩

⁴ This positive feedback loop means that the majority of our Facebook post views are of fuzzy-style content. However, this is only true for posts that get pushed out to users; for those who actively come to the ACE Facebook page for content, the ratio of fuzzy-style to utilon-style is roughly one-to-one. ↩

⁵ This is also explicitly why we do not publish cost-per-animal-spared numbers in the same way that you may see for QALYs or DALYs elsewhere. ↩

⁶ We acknowledge that there are limitations to this chart and are working on an updated version that will include both data on wild animal suffering and more clear proportions that indicate how limited animal charity donations are overall. ↩

⁷ ACE has publicly endorsed and acts in accordance with CEA’s guiding principles of effective altruism. ↩

⁸ In total, we influenced over $6 million to our recommended charities in 2017, including the $1.26 million that flowed through our Recommended Charity Fund. ↩

⁹ We are currently working on creating several more charts for non-EAs that are more shareable, and we would especially appreciate any remarks that express what level of simplification the EA community would be comfortable with. ↩